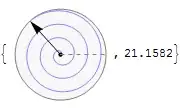
A recent SO question reminded me of some code I tried to write a while back. The aim is to make a CircularSlider[] object that can be used for angle-like variables in dynamic objects.
The framework for my solution (below) comes from the ValueThumbSlider[] defined in the Advanced Manipulate Functionality tutorial. The main difference is that in ValueThumbSlider[] the value of the slider and the position of the LocatorPlane[] are the same thing, whilst in my CircularSlider[] they are not - and this leads to problems.
The first problem is that moving the Locator will not change the slider value. This is fixed by using the 2nd argument in the Dynamic: (x = #/Abs[Complex @@ #]) &.
This in turn leads to the problem that if you externally set the value of the slider (t) from outside, it will immediately revert to its previous value. This is fixed by keeping the old value (t0) and comparing to t. If they don't match then it's assumed that t has changed and so the Locator position x is updated to its new position.
CircularSlider[t_] := CircularSlider[t, {0, 1}];
CircularSlider[Dynamic[t_], {min_, max_}] /; max > min :=
With[{d = (max - min)/(2. Pi)},
DynamicModule[{td = t/d, x, t0}, x = {Cos[td], Sin[td]};
LocatorPane[
Dynamic[If[!NumberQ[t], t = min; x = {Cos[td], Sin[td]}];
If[t != t0, t0 = t; x = {Cos[td], Sin[td]}];
t = Mod[Arg[Complex @@ x] d, max, min]; t0 = t;
x, (x = #/Abs[Complex @@ #]) &],
Graphics[{AbsoluteThickness[1.5], Circle[],
Dynamic[{Text[NumberForm[t, {3, 2}], {0, 0}]}]}],
ImageSize -> Small]]]

So my question is: can someone make this work with out the above kludges?