Forcing x axis to align with y axis in Mathematica Plot

Question

In Mathematica, when I plot things sometimes I don't always get the x-axis to line up with the exact bottom of the plot. Is there any way I can force it to do this all the time?

Here's an example of what I'm talking about: https://i.stack.imgur.com/dJPkg.png

I want the x-axis to line up perfectly with the zero tick mark way at the bottom, not in the middle of the y-axis as it is in that image.

Any way I can accomplish this?

I think it would help if you could add the mathematica statement that produced that plot/image to your question? — dbjohn, Sep 30 '11 at 21:12

score 9 · Accepted Answer · edited Apr 09 '12 at 14:25

9

Use the option AxesOrigin -> {0,0}

edited Apr 09 '12 at 14:25

Mr.Wizard

24,179
5
44
125

answered Sep 30 '11 at 21:25

Searke

779
3
3

Dr. belisarius · Answer 2 · 2011-10-01T06:39:20.040

5

The following will draw your Axes on the left and bottom, irrespective to the coordinate values:

aPlot[f_, var_, opts : OptionsPattern[]] :=
 Plot[f, var,
  AxesOrigin -> 
   First /@ (# /. AbsoluteOptions[Plot[f, var, opts], #] &@PlotRange), opts]

aPlot[Evaluate[Table[BesselJ[n, x], {n, 4}]], {x, 0, 10}, Filling -> Axis]

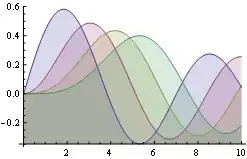
enter image description here

aPlot[Sin[x], {x, 0, 2 Pi}]

enter image description here

edited Oct 01 '11 at 06:39

answered Oct 01 '11 at 03:54

Dr. belisarius

60,527
15
115
190

@belisarius: I like your solution and Alexey Popkov's derived solution for their generality, but I want to stay away from them simply because it's so much more complicated and the alignment I need to do is easily satisfied by `AxesOrigin->{0, 0}`. It's too bad something like this isn't already built into Mathematica. – Mike Bailey Oct 11 '11 at 04:37
@Mike If all you need is the {0,0} case, obviously `AxesOrigin` is the way to go! – Dr. belisarius Oct 11 '11 at 04:41

score 4 · Answer 3 · answered Sep 30 '11 at 21:30

You could also use something like: Frame -> {{Automatic, None}, {Automatic, None}}

(Also I think that fact that it's not choosing {0,0} by default means that y=0 is being brought into range by PlotRangePadding. So that may be another option to keep an eye on.)

score 1 · Answer 4 · edited May 23 '17 at 11:53

Here is (IMO) more elegant method based on belisarius's code which uses the DisplayFunction option (see here interesting discussion on this option):

Plot[Evaluate[Table[BesselJ[n, x], {n, 4}]], {x, 0, 10}, 
 Filling -> Axis, 
 DisplayFunction -> 
  Function[{plot}, 
   Show[plot, 
    AxesOrigin -> 
     First /@ (PlotRange /. AbsoluteOptions[plot, PlotRange]), 
    DisplayFunction -> Identity]]]

The only drawback of both methods is that AbsoluteOptions does not always give correct value of PlotRange. The solution is to use the Ticks hack (which gives the complete PlotRange with explicit value of PlotRangePadding added):

completePlotRange[plot_] := 
 Last@Last@
   Reap[Rasterize[
     Show[plot, Ticks -> (Sow[{##}] &), DisplayFunction -> Identity], 
     ImageResolution -> 1]]
Plot[Evaluate[Table[BesselJ[n, x], {n, 4}]], {x, 0, 10}, 
 Filling -> Axis, 
 DisplayFunction -> 
  Function[{plot}, 
   Show[plot, AxesOrigin -> First /@ completePlotRange[plot], 
    DisplayFunction -> Identity]]]

It is interesting to note that this code gives exactly the same rendering as simply specifying Frame -> {{Automatic, None}, {Automatic, None}}, Axes -> False:

pl1 = Plot[Evaluate[Table[BesselJ[n, x], {n, 4}]], {x, 0, 10}, 
   Filling -> Axis, 
   DisplayFunction -> 
    Function[{plot}, 
     Show[plot, AxesOrigin -> First /@ completePlotRange[plot], 
      DisplayFunction -> Identity]]];
pl2 = Plot[Evaluate[Table[BesselJ[n, x], {n, 4}]], {x, 0, 10}, 
   Filling -> Axis, Frame -> {{Automatic, None}, {Automatic, None}}, 
   Axes -> False];
Rasterize[pl1] == Rasterize[pl1]

=> True

I knew about the PlotRange anomaly, but I thought it was related to some Plot[] cousins, but not to Plot[] itself. — Dr. belisarius, Oct 01 '11 at 19:56

Forcing x axis to align with y axis in Mathematica Plot

4 Answers4