Series and limits
Two important limits:
 for any real number k
for any real number k
 for all k > 0
for all k > 0
The basic series expansions







Improper intergrals
The integral : is said to be improper if
is said to be improper if
- the interval of integration is infinite, or;
- f(x) is not defined at one or both of the end points x=a and x=b, or;
- f(x) is not defined at one or more interior points of the interval
 .
.
Polar coordinates
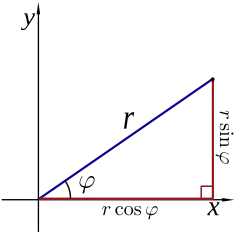 A diagram illustrating the relationship between polar and Cartesian coordinates.
A diagram illustrating the relationship between polar and Cartesian coordinates.




The area bounded by a polar curve
For the curve 


r must be defined and be non-negative throughout the interval 
Numerical methods for the solution of first order differential equations



where

and

Second order differential equations
Further reading
The AQA's free textbook [1]
