Secant, Cosecant, and Cotangent
Secant
The secant of an angle is the reciprocal of its cosine.

Cosecant
The cosecant of an angle is the reciprocal of its sine.
 [note 1]
[note 1]
Cotangent
The cotangent of an angle is the reciprocal of its tangent.

Graphs
-
Graph of sec x
-
Graph of cosec x
-
Graph of cot x
Solving Equations with Secants, Cosecants, and Cotangents
Solving an equation with secants, cosecants, or cotangents is pretty much the same method as with any other trigonometric equation.
e.g. Solve  for
for 

Identities
Cotangent identity
 and
and  , therefore
, therefore 
Pythagorean-derived identities
The Pythagorean trigonometric identity states that  . We can divide both sides by
. We can divide both sides by  to obtain another identity:
to obtain another identity:  . Alternatively, we can divide both sides by
. Alternatively, we can divide both sides by  to obtain
to obtain  .
.
The addition formulae are used when we have a trigonometric function applied to a sum or difference, e.g.  .
.
For sine, cosine, and tangent, the addition formulae are:[note 2]

The double angle formulae are a special case of the addition formulae, when both of the terms in the sum are equal.

Converting  to
to  or
or 
It is helpful when solving trigonometric equations to convert an expression into a single term. To do this, we can use the addition formulae.
e.g. Solve  for
for 

Using  is pretty similar.
is pretty similar.
e.g. Solve  for
for 

- Notes
- ↑ Some sources may use
 , but this notation is not endorsed by Cambridge
, but this notation is not endorsed by Cambridge
- ↑ The proofs of these formulae are beyond the scope of the Cambridge Syllabus, but you can read about the proofs at Wikipedia
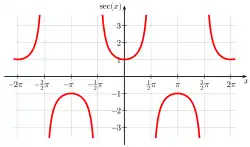 Graph of sec x
Graph of sec x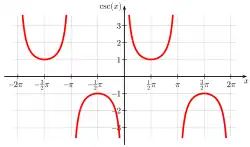 Graph of cosec x
Graph of cosec x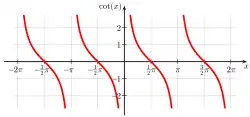 Graph of cot x
Graph of cot x