General Equations of Motion
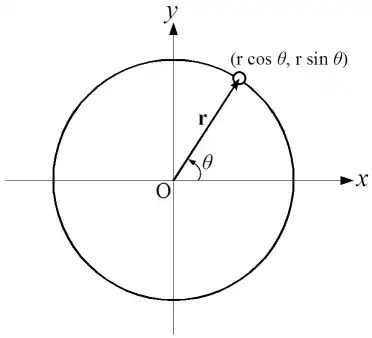
Consider a particle moving in a circle with radius  and centre at the origin O.
and centre at the origin O.
Let  denote the displacement of the particle. Using the angular displacement
denote the displacement of the particle. Using the angular displacement  (as measured from the positive
(as measured from the positive  -axis) as a parameter, we have
-axis) as a parameter, we have
![{\displaystyle \mathbf {r} =r\left[{\begin{matrix}\cos \theta \\\sin \theta \end{matrix}}\right]}](../../../_assets_/eb734a37dd21ce173a46342d1cc64c92/2c3a99f2ff7193b84582a33a1ddcfc5a497f9c17.svg) .
.
To obtain the velocity  of the particle, we differentiate
of the particle, we differentiate  wrt time
wrt time  . Applying the chain rule, we have
. Applying the chain rule, we have

|

|
|
|

|
|
|
![{\displaystyle =\left(r{\frac {d}{d\theta }}\left[{\begin{matrix}\cos \theta \\\sin \theta \end{matrix}}\right]\right)\left({\dot {\theta }}\right)}](../../../_assets_/eb734a37dd21ce173a46342d1cc64c92/1ede3934d1660a72f2ac2098014d98e3f2af9278.svg)
|
|
|
![{\displaystyle =r{\dot {\theta }}\left[{\begin{matrix}-\sin \theta \\\cos \theta \end{matrix}}\right]}](../../../_assets_/eb734a37dd21ce173a46342d1cc64c92/8f83646aa10bd5b906190924cd515f59913657d1.svg)
|
To determine the acceleration  of the particle, we differentiate
of the particle, we differentiate  wrt
wrt  and get
and get

|

|
|
|

|
|
|
![{\displaystyle =\left(r{\frac {d}{d\theta }}\left\{{\dot {\theta }}\left[{\begin{matrix}-\sin \theta \\\cos \theta \end{matrix}}\right]\right\}\right)\left({\dot {\theta }}\right)}](../../../_assets_/eb734a37dd21ce173a46342d1cc64c92/6ee42fad8b2c892772c0c1b6eabc761a1d1b5315.svg)
|
|
|
![{\displaystyle =r{\dot {\theta }}\left({\dot {\theta }}\left[{\begin{matrix}-\cos \theta \\-\sin \theta \end{matrix}}\right]+{\ddot {\theta }}\left[{\begin{matrix}-\sin \theta \\\cos \theta \end{matrix}}\right]\right)}](../../../_assets_/eb734a37dd21ce173a46342d1cc64c92/d0667a2cbaa99e97cb37caa9b89a8e4fb02ca4a2.svg)
|
|
|
![{\displaystyle =-r{\dot {\theta }}^{2}\left[{\begin{matrix}\cos \theta \\\sin \theta \end{matrix}}\right]+r{\dot {\theta }}{\ddot {\theta }}\left[{\begin{matrix}-\sin \theta \\\cos \theta \end{matrix}}\right]}](../../../_assets_/eb734a37dd21ce173a46342d1cc64c92/ab72d9d0bf3edf73745a18b31171992810c6f3ac.svg)
|
Summary
To simplify our expressions, we introduce the unit vectors ![{\displaystyle {\hat {\mathbf {r} }}=\left[{\begin{matrix}\cos \theta \\\sin \theta \end{matrix}}\right]}](../../../_assets_/eb734a37dd21ce173a46342d1cc64c92/9be89fd1709f7828d5de0ef5642ba8bb0c03fab7.svg) , and
, and ![{\displaystyle {\hat {\mathbf {n} }}=\left[{\begin{matrix}-\sin \theta \\\cos \theta \end{matrix}}\right]}](../../../_assets_/eb734a37dd21ce173a46342d1cc64c92/3173ebd13aef9c5c4b7e419d4ceeda9da11b54a5.svg) . Observe that
. Observe that  is perpendicular to
is perpendicular to  since
since  .
.
From the above derivations, we arrive at the following:
- Displacement

- Velocity

- Acceleration

|
We note the following:
- The velocity is always perpendicular to the displacement of the particle.
- The acceleration consists of a radial component directed towards the centre of the circle, and a transverse component parallel to the velocity.
If the particle moves at a constant speed in a circle, then we say that it observes uniform circular motion. For this special case, we set the angular acceleration  , and replace the angular velocity
, and replace the angular velocity  with the constant angular speed
with the constant angular speed  . Our equations of motion reduce to the following:
. Our equations of motion reduce to the following:
- Displacement

- Velocity

- Acceleration

|
We note the following:
- The velocity is always perpendicular to the displacement of the particle. Further, the speed of the particle is simply
 .
.
- The acceleration is always directed towards the centre of the circle. Its magnitude is given by
 .
.
The following diagrams describe one example of horizontal circular motion. If the particle is moving at a constant speed, then we say that it is performing uniform horizontal circular motion. To obtain the equations of motion, we apply Newton's Second Law to the resolved forces acting on the particle in the horizontal and vertical directions.
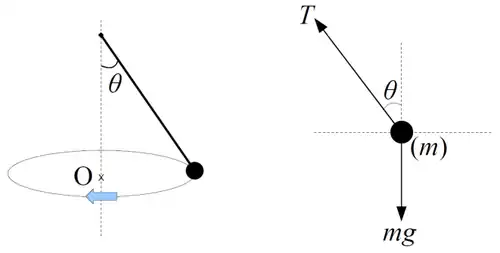
Let us assume that the particle is moving at a constant speed around a circle of radius  .
.
First, we consider the resolved forces acting on the particle in the vertical direction. Since there is no acceleration, Newton's Second Law produces:
|
|

|

|

|

|

|
Next, we consider the resolved forces acting on the particle in the horizontal direction. Since the particle is performing circular motion, its acceleration towards the centre of the circle is given by  . Thus, by Newton's Second Law, we have:
. Thus, by Newton's Second Law, we have:
|
|

|

|

|

|

|
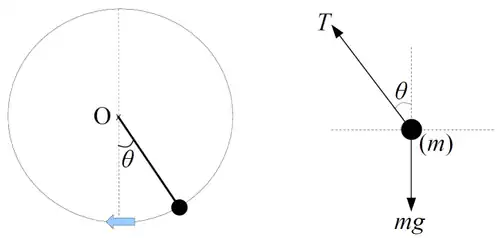
Vertical Circular Motion
The following diagrams describe one example of vertical circular motion. As before, we obtain the equations of motion by applying Newton's Second Law to the resolved forces acting on the particle in the horizontal and vertical directions. In addition, we can also use the Law of Conservation of Energy to help us relate the speed of the particle to its height.
The motion of a moving car round a circular path is being propagated by the centripetal force acting on the car which is directed towards the center of the circular path.
when we look critically into the Newton's Third Law of motion, it states that in every action, there must be a reaction which is equal to it but opposite in direction. as the car is being held on the circular path by the frictional (Centripetal) force, the car in return exerts and outward pull against the direction of the Fcentri, which is called the centrifugal force.


