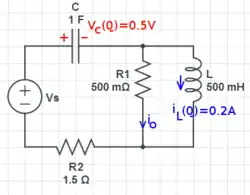
Series RLC circuit with two initial conditions Example 33 for wikibook circuit theory Find io (t) if Vs (t) = 1 + cos(3t).
Choose Starting Point
Because of the initial conditions, going to start with Vc (t) and then work our way through the initial conditions to io .
Transfer Function
H
(
s
)
=
V
c
V
s
=
1
s
C
1
s
C
+
1
1
R
1
+
1
s
L
+
R
2
{\displaystyle H(s)={\frac {V_{c}}{V_{s}}}={\frac {\frac {1}{sC}}{{\frac {1}{sC}}+{\frac {1}{{\frac {1}{R_{1}}}+{\frac {1}{sL}}}}+R_{2}}}}
The MuPad commands are going to be:
L :=1; R1:=.5; R2:=1.5; C:=.5;
simplify((1/(s*C))/(1/(s*C) + 1/(1/R1 + 1/(s*L)) + R2))
Which results in:
H
(
s
)
=
8
s
+
4
8
s
2
+
11
s
+
4
{\displaystyle H(s)={\frac {8s+4}{8s^{2}+11s+4}}}
Homogeneous Solution
Set the denominator of the transfer function to 0 and solve for s:
solve(8*s^2 + 11*s + 4)
Imaginary roots:
s
1
,
2
=
−
11
±
7
i
16
{\displaystyle s_{1,2}={\frac {-11\pm {\sqrt {7}}i}{16}}}
So the solution has the form:
V
c
h
=
e
−
11
t
16
(
A
cos
7
t
16
+
B
sin
7
t
16
)
+
C
{\displaystyle V_{c_{h}}=e^{-{\frac {11t}{16}}}(A\cos {\frac {7t}{16}}+B\sin {\frac {7t}{16}})+C}
Particular Solution
After a very long time the capacitor opens, no current flows, so all the source drop is across the capacitor. The source is a unit step function thus:
V
c
p
=
1
{\displaystyle V_{c_{p}}=1}
Initial Conditions
mupad screen shot leading up to computing constant B Adding the particular and homogenous solutions, get:
V
c
(
t
)
=
1
+
e
−
11
t
16
(
A
cos
7
t
16
+
B
sin
7
t
16
)
+
C
{\displaystyle V_{c}(t)=1+e^{-{\frac {11t}{16}}}(A\cos {\frac {7t}{16}}+B\sin {\frac {7t}{16}})+C}
Doing the final condition again, get:
V
c
(
∞
)
=
1
=
1
+
C
⇒
C
=
0
{\displaystyle V_{c}(\infty )=1=1+C\Rightarrow C=0}
Which implies that C is zero.
From the given initial conditions, know that Vc (0+ ) = 0.5 so can find A:
V
c
(
0
+
)
=
0.5
=
1
+
A
⇒
A
=
−
0.5
{\displaystyle V_{c}(0_{+})=0.5=1+A\Rightarrow A=-0.5}
Finding B is more difficult. From capacitor terminal relation:
VC := 1 + exp(-11*t/16)*(-.5*cos(7*t/16) + B*sin(7*t/16))
IT := diff(VC,t)
The total current is:
i
T
(
t
)
=
C
d
V
c
d
t
=
11
e
−
11
t
16
16
(
0.5
cos
7
t
16
−
B
sin
7
t
16
)
+
7
e
−
11
t
16
16
(
0.5
sin
7
t
16
+
B
cos
7
t
16
)
{\displaystyle i_{T}(t)=C{dV_{c} \over dt}={\frac {11e^{-{\frac {11t}{16}}}}{16}}(0.5\cos {\frac {7t}{16}}-B\sin {\frac {7t}{16}})+{\frac {7e^{-{\frac {11t}{16}}}}{16}}(0.5\sin {\frac {7t}{16}}+B\cos {\frac {7t}{16}})}
The loop equation can be solved for the voltage across the LR parallel combination:
V
C
+
V
L
R
+
R
2
C
d
V
c
d
t
−
V
s
=
0
{\displaystyle V_{C}+V_{LR}+R_{2}C{dV_{c} \over dt}-V_{s}=0}
V
L
R
=
V
s
−
V
C
−
R
2
i
t
=
1
−
V
c
−
1.5
∗
i
t
{\displaystyle V_{LR}=V_{s}-V_{C}-R_{2}i_{t}=1-V_{c}-1.5*i_{t}}
VLR := 1 - VC - 1.5*IT
We know from the inductor terminal relation that:
i
L
=
1
L
∫
V
L
R
d
t
+
C
1
{\displaystyle i_{L}={\frac {1}{L}}\int V_{LR}dt+C_{1}}
IL := 1/.5 * int(VLR,t)
At this point mupad gave up and went numeric. In any case, it is clear from t = ∞ where the inductor current has to be zero that the integration constant is zero. This enables us to compute B from the inductor initial condition.
t :=0
Set the time to zero, set IL equal to the initial condition of .2 amps and solve for B:
solve(IL=0.2, B)
And get that B is -0.2008928571 ...
mupad screen shot finding the desired output io The desired answer is io which is just VLR /R_1. To calculate need to start new mupad session because t is zero now. Start with:
B := -0.2008928571;
R1 :=0.5;
Repeat the above commands up to VLR and then add:
io = VLR/R1
i
o
=
3
e
−
11
t
16
(
0.0879
cos
7
t
16
−
0.219
sin
7
t
16
)
−
0.0625
e
−
11
t
16
(
0.5
cos
7
t
16
+
0.201
sin
7
t
16
)
{\displaystyle i_{o}=3e^{-{\frac {11t}{16}}}(0.0879\cos {\frac {7t}{16}}-0.219\sin {\frac {7t}{16}})-0.0625e^{-{\frac {11t}{16}}}(0.5\cos {\frac {7t}{16}}+0.201\sin {\frac {7t}{16}})}