Electronics Handbook/Circuits/Parallel Circuit

Electronic components R,L,C can be connected in parallel to form RL, RC, LC, RLC series circuit

1. RC Parallel
2. RL Parallel
3. LC Parallel
4. RLC Parallel

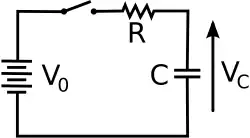
The total Impedance of the circuit

${\displaystyle Z=Z_{R}+Z_{C}=R+{\frac {1}{j\omega C}}={\frac {1+j\omega RC}{j\omega C}}}$

${\displaystyle Z={\frac {1}{j\omega C}}(1+j\omega T}$)

T = RC

At Equilibrium sum of all voltages equal zero

${\displaystyle C{\frac {dV}{dt}}+{\frac {V}{R}}=0}$

${\displaystyle {\frac {dV}{dt}}=-{\frac {1}{RC}}V}$

${\displaystyle {\frac {1}{V}}dV=-{\frac {1}{RC}}dt}$

${\displaystyle \int {\frac {1}{V}}dV=-\int {\frac {1}{RC}}dt}$

ln V = ${\displaystyle -{\frac {1}{RC}}+C}$

${\displaystyle V=e^{-}({\frac {1}{RC}})t+C}$

${\displaystyle V=Ae^{-}({\frac {1}{T}})t}$

${\displaystyle A=e^{C}}$

T = RC

Circuit's Impedance in Polar coordinate

${\displaystyle Z=Z_{R}+Z_{C}}$

${\displaystyle Z=R\angle 0+{\frac {1}{\omega C}}\angle -90}$

${\displaystyle {\sqrt {R^{2}+({\frac {1}{\omega C}})^{2}}}\angle Tan^{-}1{\frac {1}{\omega RC}}}$

Phase Angle Difference Between Voltage and Current There is a difference in angle Between Voltage and Current . Current leads Voltage by an angle θ

${\displaystyle Tan\theta ={\frac {1}{\omega RC}}={\frac {1}{2\pi fRC}}={\frac {1}{2\pi }}{\frac {t}{T}}}$

RL series circuit has a first order differential equation of voltage

${\displaystyle {\frac {d}{dt}}f(t)+{\frac {t}{T}}=0}$

Which has one real root

${\displaystyle V(t)=Ae^{\frac {-t}{T}}}$

${\displaystyle A=e^{c}}$

The Natural Response of the circuit at equilibrium is a Exponential Decrease function

Phase Angle Difference Between Voltage and Current

${\displaystyle Tan\theta ={\frac {1}{\omega RC}}={\frac {1}{2\pi fRC}}={\frac {1}{2\pi }}{\frac {t}{T}}}$

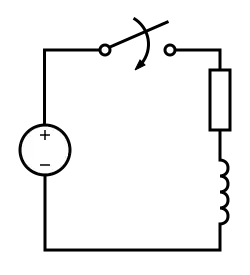
The total Circuit's Impedance In Rectangular Coordinate

${\displaystyle Z=Z_{R}+Z_{L}=R+j\omega L}$

${\displaystyle Z={\frac {1}{R}}(1+j\omega T)}$

${\displaystyle T={\frac {L}{R}}}$

At Equilibrium sum of all voltages equal zero

${\displaystyle L{\frac {dI}{dt}}+IR=0}$

${\displaystyle {\frac {dI}{dt}}=-I{\frac {R}{L}}}$

${\displaystyle \int {\frac {1}{I}}dI=-\int {\frac {L}{R}}dt}$

ln I = ${\displaystyle (-{\frac {L}{R}}+c)}$

I = ${\displaystyle e^{(}-{\frac {L}{R}}+c)t}$

I = ${\displaystyle e^{c}e^{(}-{\frac {L}{R}}t)}$

I = ${\displaystyle Ae^{(}-{\frac {L}{R}}t)}$

Circuit's Impedance In Polar Coordinate

${\displaystyle Z=Z_{R}+Z_{L}=R\angle 0+\omega L\angle 90}$

${\displaystyle {\sqrt {R^{2}+(\omega L)^{2}}}\angle Tan^{-}1\omega {\frac {L}{R}}}$

Phase Angle of Difference Between Voltage and Current

${\displaystyle Tan\theta =\omega {\frac {L}{R}}=2\pi f{\frac {L}{R}}=2\pi {\frac {T}{t}}}$

In summary RL series circuit has a first order differential equation of current

${\displaystyle {\frac {d}{dt}}f(t)+{\frac {1}{T}}=0}$

Which has one real root

${\displaystyle I(t)=Ae^{\frac {t}{T}}}$

${\displaystyle A=e^{c}}$

The Natural Response of the circuit at equilibrium is a Exponential Decrease function

Phase Angle of Difference Between Voltage and Current

${\displaystyle Tan\theta =\omega {\frac {L}{R}}=2\pi f{\frac {L}{R}}=2\pi {\frac {T}{t}}}$

The Total Circuit's Impedance in Rectangular Form

${\displaystyle Z=|Z|\angle \theta }$

${\displaystyle Z=|Z_{L}-Z_{C}|\angle \pm 90}$ . Z_L = Z_C

${\displaystyle Z=0\angle 0}$ . Z_L = Z_C

Circuit's Natural Response at equilibrium

${\displaystyle L{\frac {dI}{dt}}+{\frac {1}{C}}\int Idt=0}$

${\displaystyle {\frac {d^{2}I}{dt^{2}}}+{\frac {1}{LC}}=0}$

${\displaystyle s^{2}+{\frac {1}{LC}}=0}$

${\displaystyle s=\pm {\sqrt {\frac {1}{LC}}}t=\pm \omega t}$

${\displaystyle I=e^{(}st)}$

${\displaystyle I=e^{j}\omega t+e^{-}j\omega t}$

${\displaystyle I=ASin\omega t}$

The Natural Response at equilibrium of the circuit is a Sinusoidal Wave

At Resonance, The total Circuit's impedance is zero and the total volages are zero

${\displaystyle Z_{L}-Z_{C}=0}$

${\displaystyle \omega L={\frac {1}{\omega C}}}$

${\displaystyle \omega ={\sqrt {\frac {1}{LC}}}}$

${\displaystyle V_{L}+V_{C}=0}$

${\displaystyle V_{L}=-V_{C}}$

The Resonance Reponse of the circuit at resonance is a Standing (Sinusoidal) Wave

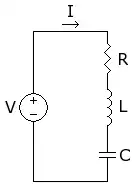
At Equilibrium, the sum of all voltages equal to zero

${\displaystyle L{\frac {dI}{dt}}+IR+{\frac {1}{C}}\int Idt=0}$

${\displaystyle {\frac {dI}{dt}}+I{\frac {R}{L}}+{\frac {1}{LC}}=0}$

${\displaystyle {\frac {d^{2}I}{dt^{2}}}+{\frac {R}{L}}{\frac {dI}{dt}}+{\frac {1}{LC}}=0}$

${\displaystyle s^{2}+{\frac {R}{L}}s+{\frac {1}{LC}}=0}$

${\displaystyle s=(-\alpha \pm \lambda )t}$

Với

${\displaystyle \alpha ={\frac {R}{2L}}}$ và

${\displaystyle \beta ={\frac {1}{LC}}}$

${\displaystyle \lambda ={\sqrt {\alpha ^{2}-\beta ^{2}}}}$

Khi ${\displaystyle \alpha ^{2}=\beta ^{2}}$

${\displaystyle s=-\alpha t}$

${\displaystyle I=e^{(}-\alpha )t}$

The response of the circuit is an Exponential Deacy

Khi ${\displaystyle \alpha ^{2}>\beta ^{2}}$

${\displaystyle s=(-\alpha \pm \lambda )t}$

${\displaystyle I=e^{-}\alpha t\pm (e^{\lambda }t+e^{-}\lambda t)}$

The response of the circuit is an Exponential Deacy

Khi ${\displaystyle \alpha ^{2}<\beta ^{2}}$

${\displaystyle s=(-\alpha \pm \lambda )t}$

${\displaystyle I=e^{-}\alpha t\pm (e^{j}\lambda t+e^{-}j\lambda t)}$

The response of the circuit is an Exponential decay sinusoidal wave

Điện Kháng Tổng Mạch Điện

${\displaystyle Z=Z_{R}+Z_{L}+Z_{C}}$

${\displaystyle Z=R+j\omega L+{\frac {1}{j\omega C}}}$

${\displaystyle Z={\frac {1}{j\omega C}}(j\omega ^{2}+j\omega {\frac {R}{L}}+{\frac {1}{LC}})}$

The total impedance of the circuit

${\displaystyle Z=Z_{R}+Z_{L}+Z_{C}=R+0=R}$

${\displaystyle I={\frac {V}{R}}}$

${\displaystyle Z_{L}=Z_{C}}$

${\displaystyle j\omega L={\frac {1}{j\omega C}}}$

${\displaystyle \omega ={\sqrt {\frac {1}{LC}}}}$

At resonance frequency ${\displaystyle \omega ={\sqrt {\frac {1}{LC}}}}$ the total impedance of the circuit is Z = R ; at its minimum value and current will be at its maximum value  : ${\displaystyle I={\frac {V}{R}}}$

Look at the circuit, at ${\displaystyle At\omega =0Z_{C}=oo}$ , Capacitor opens circuit . Therefore, current is equal to zero . At ${\displaystyle \omega =ooZ_{L}=oo}$ , Inductor opens circuit . Therefore, current is equal to zero

Series RC and RL has a Character first order differential equation of the form

${\displaystyle {\frac {df(t)}{dt}}+\omega t=0}$

that has Decay exponential function as Natural Response

${\displaystyle f(x)=Ae^{(}-{\frac {t}{T}})}$

f(t) = i(t) for series RL

f(t) = v(t) for series RC

Series LC and RLC has a Characteristic Second order differential equation of the form

${\displaystyle {\frac {d^{2}f(t)}{dt}}+\omega t=0}$

${\displaystyle f(x)=e^{(}\pm \omega t)}$

${\displaystyle f(x)=e^{(}\omega t)+e^{(}-\omega t)=ASin\omega t}$

At equilibrium , the Natural Response of the circuit is Sinusoidal Wave

${\displaystyle f(x)=ASin\omega t}$

At Equilibrum , the Resonance Response is Standing Wave Reponse