Exercise
Let  be Lipschitz continuous with Lipschitz constant
be Lipschitz continuous with Lipschitz constant  . That is
. That is

for all  . Prove that
. Prove that  is uniformly continuous.
is uniformly continuous.
Continuity at the origin
Exercise
Prove that the following function is continuous at the origin  :
:

with a real number 
How to get to the proof?
In order to establish continuity at the origin  , we make use of the epsilon-delta criterion. That means, for all
, we make use of the epsilon-delta criterion. That means, for all  we have to find a
we have to find a  such that the inequality
such that the inequality  holds at all
holds at all  with
with  . The question now is how to find a suitable
. The question now is how to find a suitable  for any given
for any given  . To answer this question, we take a look at the function
. To answer this question, we take a look at the function  around
around  :
:
Since at 
 , there is
, there is

This inequality also holds at  , since
, since  . Visually, the inequality above means that the graph of the function
. Visually, the inequality above means that the graph of the function  fits inside the "double wedge" given by
fits inside the "double wedge" given by  , where
, where  tells us, how much the wedge is "stretched" in
tells us, how much the wedge is "stretched" in  -direction. So if we choose
-direction. So if we choose  , then at any
, then at any  with
with  , there is
, there is

Which we can use to carry through the proof (see below).
Note: We can also "move the double wedge" to any  when investigating continuity at
when investigating continuity at  . If the graph fits inside the "moved double wedge"
. If the graph fits inside the "moved double wedge"  , then for any
, then for any  , there is
, there is

So any function fitting in such a double wedge is continuous. The converse does not hold true. There are functions which do not fit in any double wedge around  but are continuous at
but are continuous at  . An example is the square root function
. An example is the square root function  around
around  .
.
-
The function

is continuous at

.
-
The function

is continuous at any

.
-
The function

is not Lipschitz-continuous at

Extreme value theorem
Exercise (Maximum and minimum of a function)
Prove that the function  defined on
defined on  attains a maximum, but not a minimum.
attains a maximum, but not a minimum.
Solution (Maximum and minimum of a function)
Proof step:  attains a maximum
attains a maximum
The function  is continuous on
is continuous on  , since it is composed by continuous functions and the denominator is strictly positive (
, since it is composed by continuous functions and the denominator is strictly positive ( ). The enumerator is also strictly positive, so
). The enumerator is also strictly positive, so  for
for  ,
,  , and
, and

That means, there is an  with
with  for all
for all  . The extreme value theorem implies that
. The extreme value theorem implies that  attains a maximum on
attains a maximum on ![{\displaystyle [1,x_{0}]}](../_assets_/eb734a37dd21ce173a46342d1cc64c92/ffcdcb26a12ac1e3b6ca0a109ec4f018652fbf40.svg) . One may even show that the maximum is even global. However, computing the maximum explicitly would require us to solve
. One may even show that the maximum is even global. However, computing the maximum explicitly would require us to solve  , which is quite a computational effort and can be even harder for other functions
, which is quite a computational effort and can be even harder for other functions  . The extreme value theorem just allowed us to quickly show that there is a maximum - and saved us from the tedious solution of
. The extreme value theorem just allowed us to quickly show that there is a maximum - and saved us from the tedious solution of  .
.
Proof step:  does not attain a minimum
does not attain a minimum
Exercise (How often is a value attained #1)
- Show that there is no continuous function
 , which attains each of its function values exactly twice.
, which attains each of its function values exactly twice.
- Is there a continuous function
 , which attains each of its function values exactly three times?
, which attains each of its function values exactly three times?
Exercise (Zero of a function)
Prove that the function

has exactly one zero inside the interval ![{\displaystyle [0,{\tfrac {\pi }{2}}]}](../_assets_/eb734a37dd21ce173a46342d1cc64c92/c406038f382a4125601d91fe4ee36262cbb60fef.svg) .
.
Solution (Zero of a function)
Proof step:  has at least one zero
has at least one zero
 is continuous as it is composed by the continuous functions
is continuous as it is composed by the continuous functions  and
and  . In addition,
. In addition,

and

By means of the intermediate value theorem, there must be an ![{\displaystyle {\tilde {x}}\in [0,{\tfrac {\pi }{2}}]}](../_assets_/eb734a37dd21ce173a46342d1cc64c92/3f869afea7b1f1945f561443b546b3d575f5d844.svg) with
with  .
.
Proof step:  has exactly one zero
has exactly one zero
Exercise (Solution of an equation)
Let  with
with  . Prove that the equation
. Prove that the equation

Has at least three solutions.
Solution (Solution of an equation)
It is a powerful trick in mathematics, to transform the problem of finding solutions  to
to  as zeros of an auxiliary function
as zeros of an auxiliary function  (if
(if  , then
, then  and vice versa). In our case, the continuous auxiliary function is
and vice versa). In our case, the continuous auxiliary function is

When approaching  and
and  , this function goes to
, this function goes to

and

Therefore, there must be two arguments  with
with  and
and  (
( is close to
is close to  and
and  close to
close to  ). By the intermediate value theorem, there must hence be a zero
). By the intermediate value theorem, there must hence be a zero ![{\displaystyle {\tilde {x}}\in [x_{1},x_{2}]\subset (a,b)}](../_assets_/eb734a37dd21ce173a46342d1cc64c92/5a57df501598c92cf689fe28f87d2c94929d1fe6.svg) with
with  . This zero
. This zero  is one solution of the above equation.
is one solution of the above equation.
The same argument works between  and
and  . Since
. Since  and
and  , we can use the intermediate value theorem and get a zero
, we can use the intermediate value theorem and get a zero  with
with  .This is the second solution we have been looking for.
.This is the second solution we have been looking for.
The third solution follows by a similar argument. There is  and
and  . So the intermediate value theorem renders a
. So the intermediate value theorem renders a  with
with  . The equation has therefore at least three solutions.
. The equation has therefore at least three solutions.
Solution (Solution of an equation)
We consider the following auxiliary function:
![{\displaystyle h:[0,{\tfrac {1}{2}}]\to \mathbb {R} ,\ h(c)=f(x+{\tfrac {1}{2}})-f(x)}](../_assets_/eb734a37dd21ce173a46342d1cc64c92/ccbbf8f82c4ae0a8b4e72b5e736ec98dbb660658.svg)
Finding a ![{\displaystyle c\in [0,1]}](../_assets_/eb734a37dd21ce173a46342d1cc64c92/02b2796dc5e3cb6527d1ac6e766dc1da2ef1e120.svg) with
with  now amounts to finding a zero of
now amounts to finding a zero of  . Since
. Since  is continuous, so is
is continuous, so is  . In addition, at the endpoints of the interval, there is
. In addition, at the endpoints of the interval, there is

and

Case 1: 
Case 2: 
Exercise (Existence of exactly one zero)
Let  be a natural number. We define the function
be a natural number. We define the function  . Prove that
. Prove that  has exactly one positive zero.
has exactly one positive zero.
Solution (Existence of exactly one zero)
We need to show two things:
At first, we need to show that a zero exists inside the interval ![{\displaystyle ]0;+\infty [}](../_assets_/eb734a37dd21ce173a46342d1cc64c92/9a2b9afa8192cc3f8173fadddad0d1f5c499d881.svg) . Second, we need to assure that there is indeed only one such zero.
. Second, we need to assure that there is indeed only one such zero.
The function  is a polynomial function and hence continuous. At the beginning of the interval
is a polynomial function and hence continuous. At the beginning of the interval  , there is
, there is  i.e. the graph of the function runs below the
i.e. the graph of the function runs below the  -axis. At infinity, there is
-axis. At infinity, there is  , meaning that for large
, meaning that for large  , the graph runs above the
, the graph runs above the  -axis. As
-axis. As  is continuous, we can apply the intermediate value theorem and get a zero
is continuous, we can apply the intermediate value theorem and get a zero ![{\displaystyle x_{1}\in ]0;+\infty [}](../_assets_/eb734a37dd21ce173a46342d1cc64c92/0a24e1b870ccab8c6a2e803072884fa1fce8dc97.svg) .
.
Now we need to show that there is at most one zero. Both  and
and  are strictly monotonically increasing functions for
are strictly monotonically increasing functions for  . So we may assume that
. So we may assume that  is also strictly monotone, there.
We can prove this assumption be taking the first derivative:
is also strictly monotone, there.
We can prove this assumption be taking the first derivative:
For  there is:
there is:  .
.
One may show with a bit of effort that differentiable functions with positive derivative  are strictly monotone in the sense that
are strictly monotone in the sense that  for
for  . If there were two zeros
. If there were two zeros  , we would have
, we would have  although there is
although there is  . This would contradict
. This would contradict  being monotone and in hence excluded. Therefore,
being monotone and in hence excluded. Therefore,  can have at most one zero (as all strictly monotone functions).
can have at most one zero (as all strictly monotone functions).
Note: We could also prove that  has at most one zero, only using that
has at most one zero, only using that  is differentiable with
is differentiable with  :
:
Assume that, the function  would have two zeros
would have two zeros ![{\displaystyle x_{1},x_{2}\in ]0;+\infty [}](../_assets_/eb734a37dd21ce173a46342d1cc64c92/201c1c2873cefa352f4672a5eec3005f92682d7d.svg) with
with  .
Since the function
.
Since the function  is differentiable and
is differentiable and  , we may use Rolle's theorem and get that some
, we may use Rolle's theorem and get that some ![{\displaystyle \xi \in ]x_{1};x_{2}[}](../_assets_/eb734a37dd21ce173a46342d1cc64c92/01e4a47cb998db4453b1bc10276c7464d42295f3.svg) exists wit
exists wit  . But this is a contradiction to the first derivative of
. But this is a contradiction to the first derivative of  being strictly positive
being strictly positive  . So this is a second way to exclude the existence of two zeros.
. So this is a second way to exclude the existence of two zeros.
Continuity of the inverse function
Solution (Continuity of the inverse function 1)
Part 1:
 is continuous on
is continuous on  since it is the quotient of the continuous polynomials
since it is the quotient of the continuous polynomials  and
and  . Note that
. Note that  for all
for all  .
.
Let  with
with  . Then, strict monotonicity holds:
. Then, strict monotonicity holds:

Therefore,  is also injective.
is also injective.
Part 2: The function runs towards infinity at the end points of the open interval  as follows:
as follows:
 and
and 
Since  is continuous, the intermediate value theorem ensures that for each
is continuous, the intermediate value theorem ensures that for each  there is a
there is a  mapped onto it:
mapped onto it:  . Therefore,
. Therefore,  is also surjective:
is also surjective: ![{\displaystyle f[(-1,1)]=\mathbb {R} }](../_assets_/eb734a37dd21ce173a46342d1cc64c92/4299fa67bbb0b7a07a258d93c9fbbea94ce02d29.svg) .
.
Part 3: Since  is bijective, the inverse map exists and is bijective, as well:
is bijective, the inverse map exists and is bijective, as well:

The theorem about continuity of the inverse function tells us that  is continuous and strictly monotonically increasing. Now, let us compute
is continuous and strictly monotonically increasing. Now, let us compute  . That means, we need to bring
. That means, we need to bring  into the form
into the form  - i.e. we need to get
- i.e. we need to get  standing alone on the left side of the equation:
standing alone on the left side of the equation:

Case 1: 

Case 2: 
We can use the quadratic solution formula in order to solve for  :
:

Since  for
for  , the only reasonable solution is
, the only reasonable solution is  . Putting all together, the full definition for the inverse function reads
. Putting all together, the full definition for the inverse function reads

Exercise (Continuity of the inverse function 2)
Let

- Prove that
 is injective.
is injective.
- Determine the range
 of all attained values.
of all attained values.
- Why is the inverse function
 continuous?
continuous?
Solution (Continuity of the inverse function 2)
Part 1:
 is continuous, as it is composed by the continuous functions
is continuous, as it is composed by the continuous functions  ,
,  ,
,  and
and  on
on  .
.
The logarithm is strictly monotonically increasing (and its inverse is decreasing): for  with
with  , there is:
, there is:

Now, ![{\displaystyle {\frac {1}{\ln(x+e)}}\in (0,1]}](../_assets_/eb734a37dd21ce173a46342d1cc64c92/c3d3def8a9b3bfb4541f13dc034ea7e9d58f67ad.svg) for
for  . Since in addition,
. Since in addition,  is strictly monotonically decreasing on
is strictly monotonically decreasing on ![{\displaystyle (0,1]}](../_assets_/eb734a37dd21ce173a46342d1cc64c92/7e70f9c241f9faa8e9fdda2e8b238e288807d7a4.svg) , we have
, we have

So the  -term is also strictly monotonically increasing and so is
-term is also strictly monotonically increasing and so is  :
:

Therefore,  is also injective.
is also injective.
Part 2:
At the ends of the domain of definition, there is

and

this implies
![{\displaystyle \lim _{x\to \infty }g(x)=\lim _{x\to \infty }[\underbrace {\ln(x+e)} _{\to \infty }-\underbrace {\cos \left({\frac {1}{\ln(x+e)}}\right)} _{\to \cos(0)=1}]=\infty }](../_assets_/eb734a37dd21ce173a46342d1cc64c92/5eee71e2cf83f48c23ff3d16ea666ee30b7d9cf2.svg)
 is continuous on the interval
is continuous on the interval  . Hence, we can use a corollary of the intermediate value theorem, and get that
. Hence, we can use a corollary of the intermediate value theorem, and get that  is again an interval. Since
is again an interval. Since  is strictly monotonically increasing and
is strictly monotonically increasing and  , we can conclude
, we can conclude

Part 3:
Since  is an interval and
is an interval and  in bijective, we can use the theorem about continuity of the inverse function. I tells us that
in bijective, we can use the theorem about continuity of the inverse function. I tells us that

is indeed continuous.
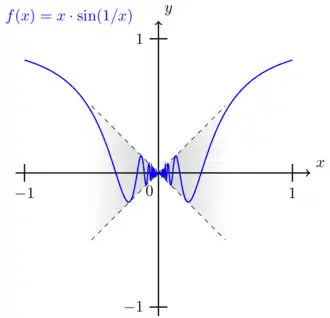 The function is continuous at .
The function is continuous at .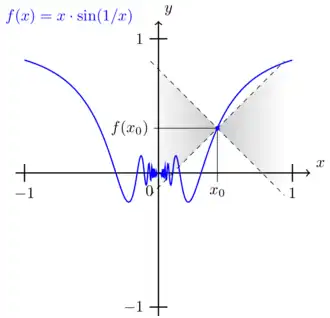 The function is continuous at any .
The function is continuous at any .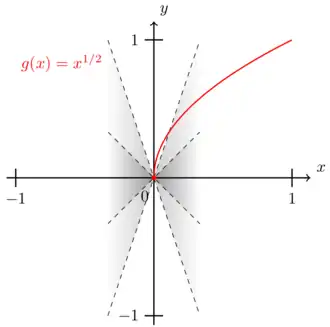 The function is not Lipschitz-continuous at
The function is not Lipschitz-continuous at