∑
k
=
0
∞
q
k
{\displaystyle \sum _{k=0}^{\infty }q^{k}}
We recall the geometric sum formula for partial sums of the geometric series. The proof of the sum formula reads as follows:
Proof (Geometrische Summenformel)
We have
∑
k
=
0
n
q
k
=
1
+
q
+
q
2
+
⋯
+
q
n
↓
multiply both side by
q
⟹
q
⋅
∑
k
=
0
n
q
k
=
q
+
q
2
+
q
3
+
⋯
+
q
n
+
1
↓
subtract second from first equation
⟹
∑
k
=
0
n
q
k
−
q
⋅
∑
k
=
0
n
q
k
=
(
1
+
q
+
⋯
+
q
n
)
−
(
q
+
q
2
+
⋯
+
q
n
+
1
)
=
1
−
q
n
+
1
↓
factor out
∑
k
=
0
n
q
k
⟹
(
1
−
q
)
⋅
∑
k
=
0
n
q
k
=
1
−
q
n
+
1
↓
⋅
1
1
−
q
, since
q
≠
1
⟹
∑
k
=
0
n
q
k
=
1
−
q
n
+
1
1
−
q
{\displaystyle {\begin{aligned}\sum _{k=0}^{n}q^{k}&=\ 1+q+q^{2}+\dotsb +q^{n}\\[0.5em]&{\color {OliveGreen}\left\downarrow \ {\text{multiply both side by }}q\right.}\\[0.5em]\implies \ q\cdot \sum _{k=0}^{n}q^{k}&=\ q+q^{2}+q^{3}+\dotsb +q^{n+1}\\[0.5em]&{\color {OliveGreen}\left\downarrow \ {\text{subtract second from first equation}}\right.}\\[0.5em]\implies \ \sum _{k=0}^{n}q^{k}-q\cdot \sum _{k=0}^{n}q^{k}&=\ (1+q+\dotsb +q^{n})-(q+q^{2}+\dotsb +q^{n+1})\\[0.5em]&=1-q^{n+1}\\[0.5em]&{\color {OliveGreen}\left\downarrow \ {\text{factor out }}\sum _{k=0}^{n}q^{k}\right.}\\[0.5em]\implies \ (1-q)\cdot \sum _{k=0}^{n}q^{k}&=\ 1-q^{n+1}\\[0.5em]&{\color {OliveGreen}\left\downarrow \ {}\cdot {\frac {1}{1-q}}{\text{, since }}q\neq 1\right.}\\[0.5em]\implies \ \sum _{k=0}^{n}q^{k}&=\ {\frac {1-q^{n+1}}{1-q}}\\[0.5em]\end{aligned}}}
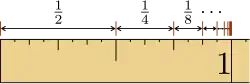
Geometric series
The geometric series
∑
k
=
0
∞
r
k
{\displaystyle \sum _{k=0}^{\infty }r^{k}}
r
=
1
2
{\displaystyle r={\tfrac {1}{2}}}
r
=
1
3
{\displaystyle r={\tfrac {1}{3}}}
r
=
1
4
{\displaystyle r={\tfrac {1}{4}}}
We consider two cases:
|
q
|
<
1
{\displaystyle |q|<1}
|
q
|
≥
1
{\displaystyle |q|\geq 1}
|
q
|
<
1
{\displaystyle |q|<1}
We consider the geometric series
∑
k
=
0
∞
q
k
{\displaystyle \sum _{k=0}^{\infty }q^{k}}
|
q
|
<
1
{\displaystyle |q|<1}
q
≠
1
{\displaystyle q\neq 1}
∑
k
=
0
∞
q
k
=
(
∑
k
=
0
n
q
k
)
n
∈
N
↓
geometric sum formula
(
q
≠
1
)
=
(
1
−
q
n
+
1
1
−
q
)
n
∈
N
{\displaystyle {\begin{aligned}\sum _{k=0}^{\infty }q^{k}&=\left(\sum _{k=0}^{n}q^{k}\right)_{n\in \mathbb {N} }\\[1em]&{\color {OliveGreen}\left\downarrow \ {\text{geometric sum formula }}(q\neq 1)\right.}\\[1em]&=\left({\frac {1-q^{n+1}}{1-q}}\right)_{n\in \mathbb {N} }\end{aligned}}}
So the geometric series converges if and only if the sequence of partial sums
(
1
−
q
n
+
1
1
−
q
)
n
∈
N
{\displaystyle \left({\tfrac {1-q^{n+1}}{1-q}}\right)_{n\in \mathbb {N} }}
(
q
n
)
n
∈
N
{\displaystyle \left(q^{n}\right)_{n\in \mathbb {N} }}
(
q
n
)
n
∈
N
{\displaystyle \left(q^{n}\right)_{n\in \mathbb {N} }}
0
{\displaystyle 0}
|
q
|
<
1
{\displaystyle |q|<1}
1
{\displaystyle 1}
q
=
1
{\displaystyle q=1}
Now, let us determine its limit:
∑
k
=
0
∞
q
k
=
lim
n
→
∞
∑
k
=
0
n
q
k
=
lim
n
→
∞
1
−
q
n
+
1
1
−
q
↓
limit theorems
=
1
−
lim
n
→
∞
q
n
+
1
1
−
q
↓
|
q
|
<
1
=
1
−
0
1
−
q
=
1
1
−
q
{\displaystyle {\begin{aligned}\sum _{k=0}^{\infty }q^{k}&=\lim _{n\to \infty }\sum _{k=0}^{n}q^{k}\\[0.3em]&=\lim _{n\to \infty }{\frac {1-q^{n+1}}{1-q}}\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{limit theorems}}\right.}\\[0.3em]&={\frac {1-\lim _{n\to \infty }q^{n+1}}{1-q}}\\[0.3em]&{\color {OliveGreen}\left\downarrow \ |q|<1\right.}\\[0.3em]&={\frac {1-0}{1-q}}\\[0.3em]&={\frac {1}{1-q}}\end{aligned}}}
Exercise (alternative proof that the geometric series converges)
Prove that the geometric series
∑
k
=
0
∞
q
k
{\displaystyle \sum _{k=0}^{\infty }q^{k}}
|
q
|
<
1
{\displaystyle |q|<1}
1
1
−
q
{\displaystyle {\tfrac {1}{1-q}}}
|
q
|
≥
1
{\displaystyle |q|\geq 1}
For
|
q
|
≥
1
{\displaystyle |q|\geq 1}
k
∈
N
0
{\displaystyle k\in \mathbb {N} _{0}}
|
q
k
|
≥
1
{\displaystyle \left|q^{k}\right|\geq 1}
(
q
k
)
k
∈
N
0
{\displaystyle \left(q^{k}\right)_{k\in \mathbb {N} _{0}}}
∑
k
=
0
∞
q
k
{\displaystyle \sum _{k=0}^{\infty }q^{k}}
The divergence becomes particularly obvious, if
q
{\displaystyle q}
q
≥
1
{\displaystyle q\geq 1}
k
∈
N
{\displaystyle k\in \mathbb {N} }
q
k
≥
1
{\displaystyle q^{k}\geq 1}
∑
k
=
1
n
q
k
≥
∑
k
=
1
n
1
=
n
{\displaystyle \sum _{k=1}^{n}q^{k}\geq \sum _{k=1}^{n}1=n}
(
n
)
n
∈
N
{\displaystyle (n)_{n\in \mathbb {N} }}
+
∞
{\displaystyle +\infty }
∑
k
=
0
∞
q
k
{\displaystyle \sum _{k=0}^{\infty }q^{k}}
Conclusion
We have learned: for
|
q
|
>
1
{\displaystyle |q|>1}
q
=
−
1
{\displaystyle q=-1}
q
=
1
{\displaystyle q=1}
|
q
|
≥
1
{\displaystyle |q|\geq 1}
|
q
|
<
1
{\displaystyle |q|<1}
1
1
−
q
{\displaystyle {\tfrac {1}{1-q}}}
Theorem (geometric series)
The geometric series
∑
k
=
0
∞
q
k
{\displaystyle \sum _{k=0}^{\infty }q^{k}}
|
q
|
<
1
{\displaystyle |q|<1}
1
1
−
q
{\displaystyle {\tfrac {1}{1-q}}}
∑
k
=
0
∞
q
k
=
{
1
1
−
q
;
|
q
|
<
1
diverges
;
|
q
|
≥
1
{\displaystyle \sum _{k=0}^{\infty }q^{k}={\begin{cases}{\frac {1}{1-q}}&;|q|<1\\{\text{diverges}}&;|q|\geq 1\end{cases}}}
Example (geometric series)
For
q
=
1
2
{\displaystyle q={\tfrac {1}{2}}}
q
=
−
1
2
{\displaystyle q=-{\tfrac {1}{2}}}
q
=
2
{\displaystyle q=2}
∑
k
=
0
∞
(
1
2
)
k
=
1
+
1
2
+
1
4
+
1
8
+
1
16
+
…
=
1
1
−
1
2
=
1
1
2
=
2
∑
k
=
0
∞
(
−
1
2
)
k
=
1
−
1
2
+
1
4
−
1
8
+
1
16
−
…
=
1
1
+
1
2
=
1
3
2
=
2
3
∑
k
=
0
∞
2
k
=
1
+
2
+
4
+
8
+
16
+
…
diverges to
+
∞
{\displaystyle {\begin{aligned}\sum _{k=0}^{\infty }\left({\frac {1}{2}}\right)^{k}&=1+{\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{8}}+{\frac {1}{16}}+\ldots ={\frac {1}{1-{\frac {1}{2}}}}={\frac {1}{\frac {1}{2}}}=2\\[1em]\sum _{k=0}^{\infty }\left(-{\frac {1}{2}}\right)^{k}&=1-{\frac {1}{2}}+{\frac {1}{4}}-{\frac {1}{8}}+{\frac {1}{16}}-\ldots ={\frac {1}{1+{\frac {1}{2}}}}={\frac {1}{\frac {3}{2}}}={\frac {2}{3}}\\[1em]\sum _{k=0}^{\infty }2^{k}&=1+2+4+8+16+\ldots \ {\text{ diverges to }}+\infty \end{aligned}}}
Example problems
Problem 1
Solution (problems: geometric series)
Solution sub-exercise 1:
∑
k
=
0
∞
1
3
k
=
∑
k
=
0
∞
1
k
3
k
=
∑
k
=
0
∞
(
1
3
)
k
↓
∑
k
=
0
∞
(
1
3
)
k
=
1
1
−
1
3
=
1
2
3
=
3
2
=
3
2
{\displaystyle {\begin{aligned}\sum _{k=0}^{\infty }{\frac {1}{3^{k}}}&=\sum _{k=0}^{\infty }{\frac {1^{k}}{3^{k}}}\\[0.5em]&=\sum _{k=0}^{\infty }\left({\frac {1}{3}}\right)^{k}\\[0.5em]&\quad {\color {OliveGreen}\left\downarrow \ \sum _{k=0}^{\infty }\left({\frac {1}{3}}\right)^{k}={\frac {1}{1-{\frac {1}{3}}}}={\frac {1}{\frac {2}{3}}}={\frac {3}{2}}\right.}\\[0.5em]&={\frac {3}{2}}\end{aligned}}}
Solution sub-exercise 2:
∑
k
=
0
∞
2
k
3
k
=
∑
k
=
0
∞
(
2
3
)
k
↓
∑
k
=
0
∞
(
2
3
)
k
=
1
1
−
2
3
=
1
1
3
=
3
=
3
{\displaystyle {\begin{aligned}\sum _{k=0}^{\infty }{\frac {2^{k}}{3^{k}}}&=\sum _{k=0}^{\infty }\left({\frac {2}{3}}\right)^{k}\\[0.5em]&\quad {\color {OliveGreen}\left\downarrow \ \sum _{k=0}^{\infty }\left({\frac {2}{3}}\right)^{k}={\frac {1}{1-{\frac {2}{3}}}}={\frac {1}{\frac {1}{3}}}=3\right.}\\[0.5em]&=3\end{aligned}}}
Solution sub-exercise 3:
∑
k
=
0
∞
(
−
2
)
k
3
k
=
∑
k
=
0
∞
(
−
2
3
)
k
↓
∑
k
=
0
∞
(
−
2
3
)
k
=
1
1
−
(
−
2
3
)
=
1
1
+
2
3
=
1
5
3
=
3
5
=
3
5
{\displaystyle {\begin{aligned}\sum _{k=0}^{\infty }{\frac {(-2)^{k}}{3^{k}}}&=\sum _{k=0}^{\infty }\left(-{\frac {2}{3}}\right)^{k}\\[0.5em]&\quad {\color {OliveGreen}\left\downarrow \ \sum _{k=0}^{\infty }\left(-{\frac {2}{3}}\right)^{k}={\frac {1}{1-(-{\frac {2}{3}})}}={\frac {1}{1+{\frac {2}{3}}}}={\frac {1}{\frac {5}{3}}}={\frac {3}{5}}\right.}\\[0.5em]&={\frac {3}{5}}\end{aligned}}}
Solution sub-exercise 5:
This series starts with
k
=
4
{\displaystyle k=4}
k
=
0
{\displaystyle k=0}
∑
k
=
4
∞
1
3
k
−
2
=
index
shift
(
∑
k
=
2
∞
1
3
k
)
=
(
∑
k
=
0
∞
1
3
k
)
−
1
3
0
−
1
3
1
=
(
∑
k
=
0
∞
(
1
3
)
k
)
−
1
−
1
3
↓
∑
k
=
0
∞
(
1
3
)
k
=
1
1
−
1
3
=
3
2
=
3
2
−
1
−
1
3
=
1
2
−
1
3
=
3
6
−
2
6
=
1
6
{\displaystyle {\begin{aligned}\sum _{k=4}^{\infty }{\frac {1}{3^{k-2}}}&{\underset {\text{shift}}{\overset {\text{index}}{=}}}\left(\sum _{k=2}^{\infty }{\frac {1}{3^{k}}}\right)\\[0.5em]&=\left(\sum _{k=0}^{\infty }{\frac {1}{3^{k}}}\right)-{\frac {1}{3^{0}}}-{\frac {1}{3^{1}}}\\[0.5em]&=\left(\sum _{k=0}^{\infty }\left({\frac {1}{3}}\right)^{k}\right)-1-{\frac {1}{3}}\\[0.5em]&\quad {\color {OliveGreen}\left\downarrow \ \sum _{k=0}^{\infty }\left({\frac {1}{3}}\right)^{k}={\frac {1}{1-{\frac {1}{3}}}}={\frac {3}{2}}\right.}\\[0.5em]&={\frac {3}{2}}-1-{\frac {1}{3}}\\[0.5em]&={\frac {1}{2}}-{\frac {1}{3}}\\[0.5em]&={\frac {3}{6}}-{\frac {2}{6}}={\frac {1}{6}}\end{aligned}}}
Problem 2
Solution (geometric series with special
q
{\displaystyle q}
Solution sub-exercise 1:
∑
k
=
0
∞
1
N
k
=
∑
k
=
0
∞
(
1
N
)
k
↓
geometric series with
q
=
1
N
=
1
1
−
1
N
=
1
N
−
1
N
=
N
N
−
1
{\displaystyle {\begin{aligned}\sum _{k=0}^{\infty }{\frac {1}{N^{k}}}&=\sum _{k=0}^{\infty }\left({\frac {1}{N}}\right)^{k}\\[0.5em]&{\color {OliveGreen}\left\downarrow \ {\text{geometric series with }}q={\frac {1}{N}}\right.}\\[0.5em]&={\frac {1}{1-{\frac {1}{N}}}}={\frac {1}{\frac {N-1}{N}}}={\frac {N}{N-1}}\end{aligned}}}
and
∑
k
=
0
∞
(
−
1
)
k
N
k
=
∑
k
=
0
∞
(
−
1
N
)
k
↓
geometric series with
q
=
−
1
N
=
1
1
+
1
N
=
1
N
+
1
N
=
N
N
+
1
{\displaystyle {\begin{aligned}\sum _{k=0}^{\infty }{\frac {(-1)^{k}}{N^{k}}}&=\sum _{k=0}^{\infty }\left(-{\frac {1}{N}}\right)^{k}\\[0.5em]&{\color {OliveGreen}\left\downarrow \ {\text{geometric series with }}q=-{\frac {1}{N}}\right.}\\[0.5em]&={\frac {1}{1+{\frac {1}{N}}}}={\frac {1}{\frac {N+1}{N}}}={\frac {N}{N+1}}\end{aligned}}}
Solution sub-exercise 2:
∑
k
=
0
∞
M
k
(
M
+
1
)
k
=
∑
k
=
0
∞
(
M
M
+
1
)
k
↓
geometric series with
q
=
M
M
+
1
=
1
1
−
M
M
+
1
=
1
1
M
+
1
=
M
+
1
{\displaystyle {\begin{aligned}\sum _{k=0}^{\infty }{\frac {M^{k}}{(M+1)^{k}}}&=\sum _{k=0}^{\infty }\left({\frac {M}{M+1}}\right)^{k}\\[0.5em]&{\color {OliveGreen}\left\downarrow \ {\text{geometric series with }}q={\frac {M}{M+1}}\right.}\\[0.5em]&={\frac {1}{1-{\frac {M}{M+1}}}}={\frac {1}{\frac {1}{M+1}}}=M+1\end{aligned}}}
and
∑
k
=
0
∞
(
−
1
)
k
M
k
(
M
+
1
)
k
=
∑
k
=
0
∞
(
−
M
M
+
1
)
k
↓
geometric series with
q
=
−
M
M
+
1
=
1
1
+
M
M
+
1
=
1
2
M
+
1
M
+
1
=
M
+
1
2
M
+
1
{\displaystyle {\begin{aligned}\sum _{k=0}^{\infty }(-1)^{k}{\frac {M^{k}}{(M+1)^{k}}}&=\sum _{k=0}^{\infty }\left(-{\frac {M}{M+1}}\right)^{k}\\[0.5em]&{\color {OliveGreen}\left\downarrow \ {\text{geometric series with }}q=-{\frac {M}{M+1}}\right.}\\[0.5em]&={\frac {1}{1+{\frac {M}{M+1}}}}={\frac {1}{\frac {2M+1}{M+1}}}={\frac {M+1}{2M+1}}\end{aligned}}}
Solution sub-exercise 3:
∑
k
=
0
∞
M
k
N
k
=
∑
k
=
0
∞
(
M
N
)
k
↓
geometric series with
q
=
M
N
=
1
1
−
M
N
=
1
N
−
M
N
=
N
N
−
M
{\displaystyle {\begin{aligned}\sum _{k=0}^{\infty }{\frac {M^{k}}{N^{k}}}&=\sum _{k=0}^{\infty }\left({\frac {M}{N}}\right)^{k}\\[0.5em]&{\color {OliveGreen}\left\downarrow \ {\text{geometric series with }}q={\frac {M}{N}}\right.}\\[0.5em]&={\frac {1}{1-{\frac {M}{N}}}}={\frac {1}{\frac {N-M}{N}}}={\frac {N}{N-M}}\end{aligned}}}
and
∑
k
=
0
∞
(
−
1
)
k
M
k
N
k
=
∑
k
=
0
∞
(
−
M
N
)
k
↓
geometric series with
q
=
−
M
N
=
1
1
+
M
N
=
1
N
+
M
N
=
N
N
+
M
{\displaystyle {\begin{aligned}\sum _{k=0}^{\infty }(-1)^{k}{\frac {M^{k}}{N^{k}}}&=\sum _{k=0}^{\infty }\left(-{\frac {M}{N}}\right)^{k}\\[0.5em]&{\color {OliveGreen}\left\downarrow \ {\text{geometric series with }}q=-{\frac {M}{N}}\right.}\\[0.5em]&={\frac {1}{1+{\frac {M}{N}}}}={\frac {1}{\frac {N+M}{N}}}={\frac {N}{N+M}}\end{aligned}}}
Problem 3
Solution (index shifting)
Solution sub-exercise 1:
∑
k
=
1
∞
q
k
=
(
∑
k
=
0
∞
q
k
)
−
q
0
=
(
∑
k
=
0
∞
q
k
)
−
1
↓
∑
k
=
0
∞
q
k
=
1
1
−
q
=
1
1
−
q
−
1
=
1
1
−
q
−
1
−
q
1
−
q
=
1
−
(
1
−
q
)
1
−
q
=
q
1
−
q
{\displaystyle {\begin{aligned}\sum _{k=1}^{\infty }q^{k}&=\left(\sum _{k=0}^{\infty }q^{k}\right)-q^{0}\\[0.5em]&=\left(\sum _{k=0}^{\infty }q^{k}\right)-1\\[0.5em]&\quad {\color {OliveGreen}\left\downarrow \ \sum _{k=0}^{\infty }q^{k}={\frac {1}{1-q}}\right.}\\[0.5em]&={\frac {1}{1-q}}-1\\[0.5em]&={\frac {1}{1-q}}-{\frac {1-q}{1-q}}\\[0.5em]&={\frac {1-(1-q)}{1-q}}\\[0.5em]&={\frac {q}{1-q}}\end{aligned}}}
Solution sub-exercise 2:
∑
k
=
2
∞
q
k
=
(
∑
k
=
0
∞
q
k
)
−
q
0
−
q
1
=
(
∑
k
=
0
∞
q
k
)
−
1
−
q
↓
∑
k
=
0
∞
q
k
=
1
1
−
q
=
1
1
−
q
−
1
−
q
=
1
1
−
q
−
1
−
q
1
−
q
−
q
(
1
−
q
)
1
−
q
=
1
−
(
1
−
q
)
−
q
(
1
−
q
)
1
−
q
=
1
−
1
+
q
−
q
+
q
2
1
−
q
=
q
2
1
−
q
{\displaystyle {\begin{aligned}\sum _{k=2}^{\infty }q^{k}&=\left(\sum _{k=0}^{\infty }q^{k}\right)-q^{0}-q^{1}\\[0.5em]&=\left(\sum _{k=0}^{\infty }q^{k}\right)-1-q\\[0.5em]&\quad {\color {OliveGreen}\left\downarrow \ \sum _{k=0}^{\infty }q^{k}={\frac {1}{1-q}}\right.}\\[0.5em]&={\frac {1}{1-q}}-1-q\\[0.5em]&={\frac {1}{1-q}}-{\frac {1-q}{1-q}}-{\frac {q(1-q)}{1-q}}\\[0.5em]&={\frac {1-(1-q)-q(1-q)}{1-q}}\\[0.5em]&={\frac {1-1+q-q+q^{2}}{1-q}}\\[0.5em]&={\frac {q^{2}}{1-q}}\end{aligned}}}
Solution sub-exercise 3:
For
|
q
|
<
1
{\displaystyle |q|<1}
m
∈
N
{\displaystyle m\in \mathbb {N} }
∑
k
=
m
∞
q
k
=
(
∑
k
=
0
∞
q
k
)
−
∑
k
=
0
m
−
1
q
k
↓
∑
k
=
0
∞
q
k
=
1
1
−
q
v
∑
k
=
0
m
−
1
q
k
=
1
−
q
m
1
−
q
=
1
1
−
q
−
1
−
q
m
1
−
q
=
1
−
(
1
−
q
m
)
1
−
q
=
1
−
1
+
q
m
1
−
q
=
q
m
1
−
q
{\displaystyle {\begin{aligned}\sum _{k=m}^{\infty }q^{k}&=\left(\sum _{k=0}^{\infty }q^{k}\right)-\sum _{k=0}^{m-1}q^{k}\\[0.5em]&\quad {\color {OliveGreen}\left\downarrow \ \sum _{k=0}^{\infty }q^{k}={\frac {1}{1-q}}{\text{ v }}\sum _{k=0}^{m-1}q^{k}={\frac {1-q^{m}}{1-q}}\right.}\\[0.5em]&={\frac {1}{1-q}}-{\frac {1-q^{m}}{1-q}}\\[0.5em]&={\frac {1-(1-q^{m})}{1-q}}\\[0.5em]&={\frac {1-1+q^{m}}{1-q}}\\[0.5em]&={\frac {q^{m}}{1-q}}\end{aligned}}}
Problem 4
Solution (Sequences which relate to the geometric series)
Solution sub-exercise 1:
For all
q
∈
R
{\displaystyle q\in \mathbb {R} }
n
∈
N
{\displaystyle n\in \mathbb {N} }
(
1
−
q
)
2
⋅
∑
k
=
0
n
(
k
+
1
)
q
k
=
1
−
(
n
+
2
)
q
n
+
1
+
(
n
+
1
)
q
n
+
2
{\displaystyle (1-q)^{2}\cdot \sum _{k=0}^{n}(k+1)q^{k}=1-(n+2)q^{n+1}+(n+1)q^{n+2}}
the left-hand side is re-arranged as follows:
(
1
−
q
)
2
⋅
∑
k
=
0
n
(
k
+
1
)
q
k
=
(
1
−
2
q
+
q
2
)
⋅
∑
k
=
0
n
(
k
+
1
)
q
k
=
(
1
−
q
−
(
q
−
q
2
)
)
⋅
∑
k
=
0
n
(
k
+
1
)
q
k
=
(
1
−
q
)
⋅
∑
k
=
0
n
(
k
+
1
)
q
k
−
(
q
−
q
2
)
⋅
∑
k
=
0
n
(
k
+
1
)
q
k
=
∑
k
=
0
n
(
k
+
1
)
q
k
−
∑
k
=
0
n
(
k
+
1
)
q
k
+
1
−
[
∑
k
=
0
n
(
k
+
1
)
q
k
+
1
−
∑
k
=
0
n
(
k
+
1
)
q
k
+
2
]
=
1
+
2
q
+
3
q
2
+
4
q
3
+
…
+
n
q
n
−
1
+
(
n
+
1
)
q
n
−
q
−
2
q
2
−
3
q
3
−
…
−
(
n
−
1
)
q
n
−
1
−
n
q
n
−
(
n
+
1
)
q
n
+
1
−
[
q
+
2
q
2
+
3
q
3
+
…
+
(
n
−
1
)
q
n
−
1
+
n
q
n
+
(
n
+
1
)
q
n
+
1
−
q
2
−
2
q
3
−
…
−
(
n
−
2
)
q
n
−
1
−
(
n
−
1
)
q
n
−
n
q
n
+
1
−
(
n
+
1
)
q
n
+
2
]
=
1
+
q
+
q
2
+
q
3
+
…
+
q
n
−
1
+
q
n
−
(
n
+
1
)
q
n
+
1
−
[
q
+
q
2
+
q
3
+
…
+
q
n
−
1
+
q
n
+
q
n
+
1
−
(
n
+
1
)
q
n
+
2
]
↓
telescoping sum
=
1
−
(
n
+
2
)
q
n
+
1
+
(
n
+
1
)
q
n
+
2
{\displaystyle {\begin{aligned}(1-q)^{2}\cdot \sum _{k=0}^{n}(k+1)q^{k}&=(1-2q+q^{2})\cdot \sum _{k=0}^{n}(k+1)q^{k}\\[0.5em]&=(1-q-(q-q^{2}))\cdot \sum _{k=0}^{n}(k+1)q^{k}\\[0.5em]&=(1-q)\cdot \sum _{k=0}^{n}(k+1)q^{k}-(q-q^{2})\cdot \sum _{k=0}^{n}(k+1)q^{k}\\[0.5em]&=\sum _{k=0}^{n}(k+1)q^{k}-\sum _{k=0}^{n}(k+1)q^{k+1}-\left[\sum _{k=0}^{n}(k+1)q^{k+1}-\sum _{k=0}^{n}(k+1)q^{k+2}\right]\\[0.5em]&={\color {OliveGreen}1+2q+3q^{2}+4q^{3}+\ldots +nq^{n-1}+(n+1)q^{n}}\\[0.5em]&\quad {\color {Red}-q-2q^{2}-3q^{3}-\ldots -(n-1)q^{n-1}-nq^{n}-(n+1)q^{n+1}}\\[0.5em]&\quad -\left[{\color {OliveGreen}q+2q^{2}+3q^{3}+\ldots +(n-1)q^{n-1}+nq^{n}+(n+1)q^{n+1}}\right.\\[0.5em]&\qquad \left.{\color {Red}-q^{2}-2q^{3}-\ldots -(n-2)q^{n-1}-(n-1)q^{n}-nq^{n+1}-(n+1)q^{n+2}}\right]\\[0.5em]&=1+q+q^{2}+q^{3}+\ldots +q^{n-1}+q^{n}-(n+1)q^{n+1}\\[0.5em]&\quad -[q+q^{2}+q^{3}+\ldots +q^{n-1}+q^{n}+q^{n+1}-(n+1)q^{n+2}]\\[0.5em]&{\color {OliveGreen}\left\downarrow \ {\text{telescoping sum}}\right.}\\[0.5em]&=1-(n+2)q^{n+1}+(n+1)q^{n+2}\end{aligned}}}
Solution sub-exercise 3:
We re-use the solution to sub-exercise 2 with
q
=
1
2
{\displaystyle q={\tfrac {1}{2}}}
∑
k
=
0
∞
k
+
1
2
k
=
∑
k
=
0
∞
(
k
+
1
)
(
1
2
)
k
↓
sub-exercise 2
=
1
(
1
−
1
2
)
2
=
1
(
1
2
)
2
=
1
1
4
=
4
{\displaystyle {\begin{aligned}\sum _{k=0}^{\infty }{\frac {k+1}{2^{k}}}&=\sum _{k=0}^{\infty }(k+1)\left({\frac {1}{2}}\right)^{k}\\[0.5em]&{\color {OliveGreen}\left\downarrow \ {\text{sub-exercise 2}}\right.}\\[0.5em]&={\frac {1}{(1-{\frac {1}{2}})^{2}}}\\[0.5em]&={\frac {1}{({\frac {1}{2}})^{2}}}={\frac {1}{\frac {1}{4}}}=4\end{aligned}}}
The second limit also follows from
q
=
1
2
{\displaystyle q={\tfrac {1}{2}}}
∑
k
=
1
∞
k
2
k
=
index-
shift
∑
k
=
0
∞
(
k
+
1
)
(
1
2
)
k
+
1
=
∑
k
=
0
∞
(
k
+
1
)
(
1
2
)
k
1
2
=
1
2
∑
k
=
0
∞
(
k
+
1
)
(
1
2
)
k
↓
sub-exercise 2
=
1
2
1
(
1
−
1
2
)
2
=
1
2
1
1
4
=
4
2
=
2
{\displaystyle {\begin{aligned}\sum _{k=1}^{\infty }{\frac {k}{2^{k}}}&{\underset {\text{shift}}{\overset {\text{index-}}{=}}}\sum _{k=0}^{\infty }(k+1)\left({\frac {1}{2}}\right)^{k+1}\\[0.5em]&=\sum _{k=0}^{\infty }(k+1)\left({\frac {1}{2}}\right)^{k}{\frac {1}{2}}\\[0.5em]&={\frac {1}{2}}\sum _{k=0}^{\infty }(k+1)\left({\frac {1}{2}}\right)^{k}\\[0.5em]&{\color {OliveGreen}\left\downarrow \ {\text{sub-exercise 2}}\right.}\\[0.5em]&={\frac {1}{2}}{\frac {1}{(1-{\frac {1}{2}})^{2}}}\\[0.5em]&={\frac {1}{2}}{\frac {1}{\frac {1}{4}}}={\frac {4}{2}}=2\end{aligned}}}
Solution (Alternative proof to sub-exercise 3)
We may also add and subtract a 1:
∑
k
=
1
∞
k
2
k
=
∑
k
=
0
∞
k
(
1
2
)
k
=
∑
k
=
0
∞
(
k
+
1
−
1
)
(
1
2
)
k
↓
series
∑
k
=
0
∞
(
k
+
1
)
(
1
2
)
k
and
∑
k
=
0
∞
(
1
2
)
k
converge
=
∑
k
=
0
∞
(
k
+
1
)
(
1
2
)
k
−
∑
k
=
0
∞
(
1
2
)
k
↓
sub-exercise 2 with
q
=
1
2
=
1
(
1
−
1
2
)
2
−
∑
k
=
0
∞
(
1
2
)
k
↓
geometric series
=
1
(
1
−
1
2
)
2
−
1
1
−
1
2
=
1
1
4
−
1
1
2
=
4
−
2
=
2
{\displaystyle {\begin{aligned}\sum _{k=1}^{\infty }{\frac {k}{2^{k}}}&=\sum _{k=0}^{\infty }k\left({\frac {1}{2}}\right)^{k}\\[0.5em]&=\sum _{k=0}^{\infty }(k+1-1)\left({\frac {1}{2}}\right)^{k}\\[0.5em]&{\color {OliveGreen}\left\downarrow \ {\text{series }}\sum _{k=0}^{\infty }(k+1)\left({\frac {1}{2}}\right)^{k}{\text{ and }}\sum _{k=0}^{\infty }\left({\frac {1}{2}}\right)^{k}{\text{ converge}}\right.}\\[0.5em]&=\sum _{k=0}^{\infty }(k+1)\left({\frac {1}{2}}\right)^{k}-\sum _{k=0}^{\infty }\left({\frac {1}{2}}\right)^{k}\\[0.5em]&{\color {OliveGreen}\left\downarrow \ {\text{sub-exercise 2 with }}q={\tfrac {1}{2}}\right.}\\[0.5em]&={\frac {1}{(1-{\frac {1}{2}})^{2}}}-\sum _{k=0}^{\infty }\left({\frac {1}{2}}\right)^{k}\\[0.5em]&{\color {OliveGreen}\left\downarrow \ {\text{geometric series}}\right.}\\[0.5em]&={\frac {1}{(1-{\frac {1}{2}})^{2}}}-{\frac {1}{1-{\frac {1}{2}}}}\\[0.5em]&={\frac {1}{\frac {1}{4}}}-{\frac {1}{\frac {1}{2}}}=4-2=2\end{aligned}}}
Hint
Analogously to sub-exercise 3, one may show for every
|
q
|
<
1
{\displaystyle |q|<1}
∑
k
=
1
∞
k
q
k
=
q
(
1
−
q
)
2
{\displaystyle \sum _{k=1}^{\infty }kq^{k}={\frac {q}{(1-q)^{2}}}}
just replace
1
2
{\displaystyle {\tfrac {1}{2}}}
q
{\displaystyle q}