Statistics/Distributions/Student-t

Student’s t

Probability density function
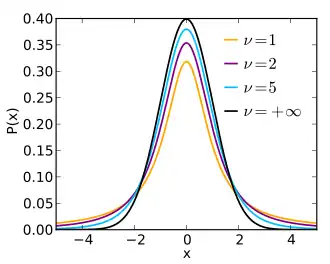
Cumulative distribution function
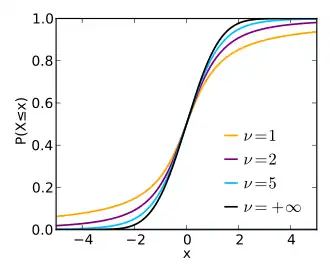
Parameters	ν > 0 degrees of freedom (real)
Support	x ∈ (−∞; +∞)
PDF	${\displaystyle \textstyle {\frac {\Gamma \left({\frac {\nu +1}{2}}\right)}{{\sqrt {\nu \pi }}\,\Gamma \left({\frac {\nu }{2}}\right)}}\left(1+{\frac {x^{2}}{\nu }}\right)^{-{\frac {\nu +1}{2}}}\!}$
CDF	${\displaystyle {\begin{matrix}{\frac {1}{2}}+x\Gamma \left({\frac {\nu +1}{2}}\right)\cdot \\[0.5em]{\frac {\,_{2}F_{1}\left({\frac {1}{2}},{\frac {\nu +1}{2}};{\frac {3}{2}};-{\frac {x^{2}}{\nu }}\right)}{{\sqrt {\pi \nu }}\,\Gamma \left({\frac {\nu }{2}}\right)}}\end{matrix}}}$ where 2F1 is the hypergeometric function
Mean	0 for ν > 1, otherwise undefined
Median	0
Mode	0
Variance	${\displaystyle \textstyle {\frac {\nu }{\nu -2}}}$ for ν > 2, ∞ for 1 < ν ≤ 2, otherwise undefined
Skewness	0 for ν > 3, otherwise undefined
Ex. kurtosis	${\displaystyle \textstyle {\frac {6}{\nu -4}}}$ for ν > 4, ∞ for 2 < ν ≤ 4, otherwise undefined
Entropy	...
MGF	undefined
CF	${\displaystyle \textstyle {\frac {K_{\nu /2}\left({\sqrt {\nu }}|t|)({\sqrt {\nu }}|t|\right)^{\nu /2}}{\Gamma (\nu /2)2^{\nu /2-1}}}}$ for ν > 0 ${\displaystyle K_{\nu }}$(x): Bessel function[1]

Student t-distribution (or just t-distribution for short) is derived from the chi-square and normal distributions. We divide the standard normally distributed value of one variable over the root of a chi-square value over its r degrees of freedom. Mathematically, this appears as:

${\displaystyle t={\frac {\mbox{Z}}{\sqrt {\chi _{r}^{2}/r}}}}$

where ${\displaystyle Z={\frac {X-{\bar {X}}}{\sigma }}}$ and ${\displaystyle \chi _{r}^{2}=\chi _{r_{1}}^{2}+...+\chi _{r_{n}}^{2}}$.

• Interactive Student-T Distribution Web Applet (Java)

1. ↑ Hurst, Simon, The Characteristic Function of the Student-t Distribution, Financial Mathematics Research Report No. FMRR006-95, Statistics Research Report No. SRR044-95