What part of Hindley-Milner do you not understand?

Question

I swear there used to be a T-shirt for sale featuring the immortal words:

---

What part of

do you not understand?

---

In my case, the answer would be... all of it!

In particular, I often see notation like this in Haskell papers, but I have no clue what any of it means. I have no idea what branch of mathematics it's supposed to be.

I recognize the letters of the Greek alphabet of course and symbols such as "∉" (which usually means that something is not an element of a set).

On the other hand, I've never seen "⊢" before (Wikipedia claims it might mean "partition"). I'm also unfamiliar with the use of the vinculum here. (Usually, it denotes a fraction, but that does not appear to be the case here.)

If somebody could at least tell me where to start looking to comprehend what this sea of symbols means, that would be helpful.

Answer 1

• The horizontal bar means that "[above] implies [below]".
• If there are multiple expressions in [above], then consider them anded together; all of the [above] must be true in order to guarantee the [below].
• : means has type
• ∈ means is in. (Likewise ∉ means "is not in".)
• Γ is usually used to refer to an environment or context; in this case it can be thought of as a set of type annotations, pairing an identifier with its type. Therefore x : σ ∈ Γ means that the environment Γ includes the fact that x has type σ.
• ⊢ can be read as proves or determines. Γ ⊢ x : σ means that the environment Γ determines that x has type σ.
• , is a way of including specific additional assumptions into an environment Γ.
  Therefore, Γ, x : τ ⊢ e : τ' means that environment Γ, with the additional, overriding assumption that x has type τ, proves that e has type τ'.

---

As requested: operator precedence, from highest to lowest:

• Language-specific infix and mixfix operators, such as λ x . e, ∀ α . σ, and τ → τ', let x = e0 in e1, and whitespace for function application.
• :
• ∈ and ∉
• , (left-associative)
• ⊢
• whitespace separating multiple propositions (associative)
• the horizontal bar

Answer 2

This syntax, while it may look complicated, is actually fairly simple. The basic idea comes from formal logic: the whole expression is an implication with the top half being the assumptions and the bottom half being the result. That is, if you know that the top expressions are true, you can conclude that the bottom expressions are true as well.

Symbols

Another thing to keep in mind is that some letters have traditional meanings; particularly, Γ represents the "context" you're in—that is, what the types of other things you've seen are. So something like Γ ⊢ ... means "the expression ... when you know the types of every expression in Γ.

The ⊢ symbol essentially means that you can prove something. So Γ ⊢ ... is a statement saying "I can prove ... in a context Γ. These statements are also called type judgements.

Another thing to keep in mind: in math, just like ML and Scala, x : σ means that x has type σ. You can read it just like Haskell's x :: σ.

What each rule means

So, knowing this, the first expression becomes easy to understand: if we know that x : σ ∈ Γ (that is, x has some type σ in some context Γ), then we know that Γ ⊢ x : σ (that is, in Γ, x has type σ). So really, this isn't telling you anything super-interesting; it just tells you how to use your context.

The other rules are also simple. For example, take [App]. This rule has two conditions: e₀ is a function from some type τ to some type τ' and e₁ is a value of type τ. Now you know what type you will get by applying e₀ to e₁! Hopefully this isn't a surprise :).

The next rule has some more new syntax. Particularly, Γ, x : τ just means the context made up of Γ and the judgement x : τ. So, if we know that the variable x has a type of τ and the expression e has a type τ', we also know the type of a function that takes x and returns e. This just tells us what to do if we've figured out what type a function takes and what type it returns, so it shouldn't be surprising either.

The next one just tells you how to handle let statements. If you know that some expression e₁ has a type τ as long as x has a type σ, then a let expression which locally binds x to a value of type σ will make e₁ have a type τ. Really, this just tells you that a let statement essentially lets you expand the context with a new binding—which is exactly what let does!

The [Inst] rule deals with sub-typing. It says that if you have a value of type σ' and it is a sub-type of σ (⊑ represents a partial ordering relation) then that expression is also of type σ.

The final rule deals with generalizing types. A quick aside: a free variable is a variable that is not introduced by a let-statement or lambda inside some expression; this expression now depends on the value of the free variable from its context.The rule is saying that if there is some variable α which is not "free" in anything in your context, then it is safe to say that any expression whose type you know e : σ will have that type for any value of α.

How to use the rules

So, now that you understand the symbols, what do you do with these rules? Well, you can use these rules to figure out the type of various values. To do this, look at your expression (say f x y) and find a rule that has a conclusion (the bottom part) that matches your statement. Let's call the thing you're trying to find your "goal". In this case, you would look at the rule that ends in e₀ e₁. When you've found this, you now have to find rules proving everything above the line of this rule. These things generally correspond to the types of sub-expressions, so you're essentially recursing on parts of the expression. You just do this until you finish your proof tree, which gives you a proof of the type of your expression.

So all these rules do is specify exactly—and in the usual mathematically pedantic detail :P—how to figure out the types of expressions.

Now, this should sound familiar if you've ever used Prolog—you're essentially computing the proof tree like a human Prolog interpreter. There is a reason Prolog is called "logic programming"! This is also important as the first way I was introduced to the H-M inference algorithm was by implementing it in Prolog. This is actually surprisingly simple and makes what's going on clear. You should certainly try it.

Note: I probably made some mistakes in this explanation and would love it if somebody would point them out. I'll actually be covering this in class in a couple of weeks, so I'll be more confident then :P.

Answer 3

if somebody could at least tell me where to start looking to comprehend what this sea of symbols means

See "Practical Foundations of Programming Languages.", chapters 2 and 3, on the style of logic through judgements and derivations. The entire book is now available on Amazon.

Chapter 2

Inductive Definitions

Inductive definitions are an indispensable tool in the study of programming languages. In this chapter we will develop the basic framework of inductive definitions, and give some examples of their use. An inductive definition consists of a set of rules for deriving judgments, or assertions, of a variety of forms. Judgments are statements about one or more syntactic objects of a specified sort. The rules specify necessary and sufficient conditions for the validity of a judgment, and hence fully determine its meaning.

2.1 Judgments

We start with the notion of a judgment, or assertion about a syntactic object. We shall make use of many forms of judgment, including examples such as these:

• n nat — n is a natural number
• n = n1 + n2 — n is the sum of n1 and n2
• τ type — τ is a type
• e : τ — expression e has type τ
• e ⇓ v — expression e has value v

A judgment states that one or more syntactic objects have a property or stand in some relation to one another. The property or relation itself is called a judgment form, and the judgment that an object or objects have that property or stand in that relation is said to be an instance of that judgment form. A judgment form is also called a predicate, and the objects constituting an instance are its subjects. We write a J for the judgment asserting that J holds of a. When it is not important to stress the subject of the judgment, (text cuts off here)

Answer 4

How do I understand the Hindley-Milner rules?

Hindley-Milner is a set of rules in the form of sequent calculus (not natural deduction) that demonstrates that we can deduce the (most general) type of a program from the construction of the program without explicit type declarations.

The symbols and notation

First, let's explain the symbols, and discuss operator precedence

• is an identifier (informally, a variable name).

• : means is a type of (informally, an instance of, or "is-a").

• (sigma) is an expression that is either a variable or function.

• thus : is read " is-a "

• ∈ means "is an element of"

• (Gamma) is an environment.

• ⊦ (the assertion sign) means asserts (or proves, but contextually "asserts" reads better.)

• ⊦ : is thus read " asserts that , is-a "

• is an actual instance (element) of type .

• (tau) is a type: either basic, variable (), functional →', or product ×' (product is not used here)

• →' is a functional type where and ' are potentially different types.

• . means (lambda) is an anonymous function that takes an argument, , and returns an expression, .

• let = ₀ in ₁ means in expression, ₁, substitute ₀ wherever appears.

• ⊑ means the prior element is a subtype (informally - subclass) of the latter element.

• is a type variable.

• ∀ . is a type, ∀ (for all) argument variables, , returning expression

• ∉ free() means not an element of the free type variables of defined in the outer context. (Bound variables are substitutable.)

Everything above the line is the premise, everything below is the conclusion (Per Martin-Löf)

Precedence, by example

I have taken some of the more complex examples from the rules and inserted redundant parentheses that show precedence:

• : ∈ could be written ( : ) ∈

• ⊦ : could be written ⊦ ( : )

• ⊦ let = ₀ in ₁ : is equivalently ⊦ ((let ( = ₀) in ₁) : )

• ⊦ . : →' is equivalently ⊦ ((.) : (→'))

Then, large spaces separating assertion statements and other preconditions indicates a set of such preconditions, and finally the horizontal line separating premise from conclusion brings up the end of the precedence order.

The Rules

What follows here are English interpretations of the rules, each followed by a loose restatement and an explanation.

Variable

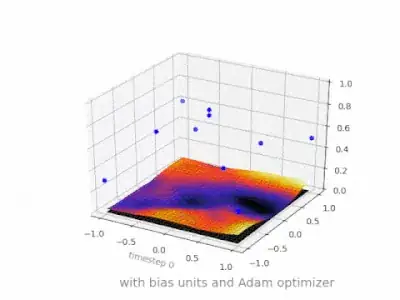
Given is a type of (sigma), an element of (Gamma),
conclude asserts is a .

Put another way, in , we know is of type because is of type in .

This is basically a tautology. An identifier name is a variable or a function.

Function Application

Given asserts ₀ is a functional type and asserts ₁ is a
conclude asserts applying function ₀ to ₁ is a type '

To restate the rule, we know that function application returns type ' because the function has type →' and gets an argument of type .

This means that if we know that a function returns a type, and we apply it to an argument, the result will be an instance of the type we know it returns.

Function Abstraction

Given and of type asserts is a type, '
conclude asserts an anonymous function, of returning expression, is of type →'.

Again, when we see a function that takes and returns an expression , we know it's of type →' because (a ) asserts that is a '.

If we know is of type and thus an expression is of type ', then a function of returning expression is of type →'.

Let variable declaration

Given asserts ₀, of type , and and , of type , asserts ₁ of type
conclude asserts let =₀ in ₁ of type

Loosely, is bound to ₀ in ₁ (a ) because ₀ is a , and is a that asserts ₁ is a .

This means if we have an expression ₀ that is a (being a variable or a function), and some name, , also a , and an expression ₁ of type , then we can substitute ₀ for wherever it appears inside of ₁.

Instantiation

Given asserts of type ' and ' is a subtype of
conclude asserts is of type

An expression, is of parent type because the expression is subtype ', and is the parent type of '.

If an instance is of a type that is a subtype of another type, then it is also an instance of that super-type - the more general type.

Generalization

Given asserts is a and is not an element of the free variables of ,
conclude asserts , type for all argument expressions returning a expression

So in general, is typed for all argument variables () returning , because we know that is a and is not a free variable.

This means we can generalize a program to accept all types for arguments not already bound in the containing scope (variables that are not non-local). These bound variables are substitutable.

Putting it all together

Given certain assumptions (such as no free/undefined variables, a known environment, ) we know the types of:

• atomic elements of our programs (Variable),
• values returned by functions (Function Application),
• functional constructs (Function Abstraction),
• let bindings (Let Variable Declarations),
• parent types of instances (Instantiation), and
• all expressions (Generalization).

Conclusion

These rules combined allow us to prove the most general type of an asserted program, without requiring type annotations.

Answer 5

The notation comes from natural deduction.

⊢ symbol is called turnstile.

The 6 rules are very easy.

Var rule is rather trivial rule - it says that if type for identifier is already present in your type environment, then to infer the type you just take it from the environment as is.

App rule says that if you have two identifiers e0 and e1 and can infer their types, then you can infer the type of application e0 e1. The rule reads like this if you know that e0 :: t0 -> t1 and e1 :: t0 (the same t0!), then application is well-typed and the type is t1.

Abs and Let are rules to infer types for lambda-abstraction and let-in.

Inst rule says that you can substitute a type with less general one.

Answer 6

There are two ways to think of e : σ. One is "the expression e has type σ", another is "the ordered pair of the expression e and the type σ".

View Γ as the knowledge about the types of expressions, implemented as a set of pairs of expression and type, e : σ.

The turnstile ⊢ means that from the knowledge on the left, we can deduce what's on the right.

The first rule [Var] can thus be read:
If our knowledge Γ contains the pair e : σ, then we can deduce from Γ that e has type σ.

The second rule [App] can be read:
If we from Γ can deduce that e_0 has the type τ → τ', and we from Γ can deduce that e_1 has the type τ, then we from Γ can deduce that e_0 e_1 has the type τ'.

It's common to write Γ, e : σ instead of Γ ∪ {e : σ}.

The third rule [Abs] can thus be read:
If we from Γ extended with x : τ can deduce that e has type τ', then we from Γ can deduce that λx.e has the type τ → τ'.

The fourth rule [Let] is left as an exercise. :-)

The fifth rule [Inst] can be read:
If we from Γ can deduce that e has type σ', and σ' is a subtype of σ, then we from Γ can deduce that e has type σ.

The sixth and last rule [Gen] can be read:
If we from Γ can deduce that e has type σ, and α is not a free type variable in any of the types in Γ, then we from Γ can deduce that e has type ∀α σ.