1

I am studying for tomorrows exam and I have checked many tutorials telling how to convert NFA to Regex but I can't seem to confirm my answers. Following the tutorials, I solved that NFA

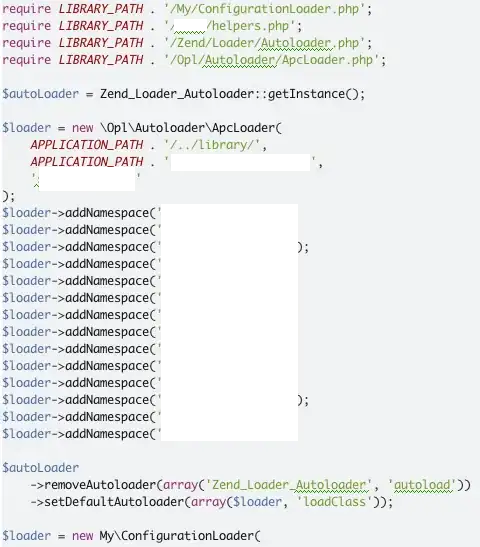
enter image description here

My solution was:

aba

Am I correct?

dlock
  • 9,447
  • 9
  • 47
  • 67
  • 1
    Depends on the algorithm you learned in class. If I were the TA, I'd only accept the regular expression obtained from executing the algorithm correctly... which might be different, contain + and parentheses, etc. – Patrick87 Jan 11 '13 at 21:54
  • The algorithm I learned in class covered converting the automata to GNFA then reducing by eliminating one state at a time. – dlock Jan 11 '13 at 21:56

2 Answers2

2

How to convert NFA to Regular Expression?

Your answer a*ba* is Correct. I can drive your answer from NFA in given image as follows:

  • There is a self loop on start state q0 with label a. So there can be any number of as are possible at initial (prefix) including null ^ in RE. So Regular Expression(RE) start with a*.

  • You need only one b to reach to final state. Actually for an accepting string; there must be at-least one b in string of a and b. So RE a*b to reach to either q1 or q2. Both are final states.

  • Once you reach to a final state (q1 or q2). No other b is possible in string (there is no outgoing edge for b from q1 and q2).

  • Only symbol is a can be possible at q1 and q2. Also for, a at q1 or at q2 move switch between q1 , q2 and both are final. So after symbol b any number of as can be in suffix. (So string ends with a* ).

And RE is a*ba*.

Also, its DFA is as follows: 

 DFA: 
======

    a-          a-  
    ||          ||
    ▼|          ▼|
--►(q0)---b---►((q1))      

    a*    b      a*    :RE  
                       ====

  • Any number of as at q0 that is: a*

  • once you get b you can switch to final state q1: b

  • at final state any number of a is possible: a*

And its a Minimized DFA!

Here is some more interesting answer by me on FAs and REs, I believe will be useful to you:

  1. HOW TO WRITE REGULAR EXPRESSION FOR A DFA
  2. RE TO DFA
  3. Regular Expression to DFA
  4. Constructing an equivalent Regular Grammar from a Regular Expression
  5. How to Eliminate Left recursion in Context-Free-Grammar
  6. Is a* the same as (a*)*?
  7. IN CONTEXT OF REGULAR EXPRESSION: is (AB)* = A*B*?
Community
  • 1
  • 1
Grijesh Chauhan
  • 57,103
  • 20
  • 141
  • 208
1

That answer is correct, in that both of the following are true:

  • Any string matching the regular expression causes the NFA to end in an accepting state (double circled state)
  • Any string causing the NFA to end in an accepting state also matches the regular expression

However, I can't check your work because you haven't posted any.

Borealid
  • 95,191
  • 9
  • 106
  • 122