15

I have a large (multi-GB) array in Matlab, that I want to truncate¹. Naively, I thought that truncating can't need much memory, but then I realised that it probably can:

>> Z = zeros(628000000, 1, 'single');
>> Z(364000000:end) = [];
Out of memory. Type HELP MEMORY for your options.

Unless Matlab does some clever optimisations, before truncating Z, this code actually creates an array (of type double!) 364000000:628000000. I don't need this array, so I can do instead:

>> Z = Z(1:363999999);

In this case, the second example works, and is fine for my purpose. But why does it work? If Z(364000000:end) = 0 fails due to the memory needed for the intermediate array 364000000:628000000, then why does not Z = Z(1:363999999) fail due to the memory needed for the intermediate array 1:363999999, that is larger? Of course, I don't need this intermediate array, and would be happy with either a solution that truncates my array without having any intermediate array, or, failing that, if Matlab optimises a particular method.

  • Is there any way to truncate an array without creating an intermediate indexing array?
  • If not, is either of the aforementioned methods more memory-efficient than the other (it appears ot is)? If so, why? Does Matlab really create intermediate arrays in both examples?

¹Reason: I'm processing data but don't know how much to preallocate. I make an educated guess, often I'm allocating too much. I choose chunk size based on available memory, because splitting in fewer chunks means faster code. So I want to avoid any needless memory usage. See also this post on allocating by chunk.

Community
  • 1
  • 1
gerrit
  • 24,025
  • 17
  • 97
  • 170
  • 3
    Some good questions here. However, it may no longer be necessary to allocate in chunks, as [it seems likely that MATLAB does this](http://stackoverflow.com/a/19061025/2778484) already in recent versions, although details from MathWorks are sparse. – chappjc Oct 28 '13 at 15:04
  • 1
    @chappjc Ah, interesting. I was not aware that this had changed. However, there may still be cases where one would want to truncate a large array. – gerrit Oct 28 '13 at 15:45
  • Agreed. I was just trying to profile your example with `profile('-memory','on');` when I crashed my computer! – chappjc Oct 28 '13 at 15:47
  • 1
    here's an interesting thread on that matter http://www.mathworks.com/matlabcentral/newsreader/view_thread/253015 – bla Oct 28 '13 at 18:31
  • Without having any sources, I'm pretty sure that Matlab does those clever optimizations, and your second command does not generate an intermediate array. – A. Donda Oct 28 '13 at 18:44
  • @natan Interesting. It appears the most efficient way would be a mex-function, also considering three more linked threads [1](http://www.mathworks.com/matlabcentral/newsreader/view_thread/245581#631580), [2](http://www.mathworks.com/matlabcentral/newsreader/view_thread/241591), [3](http://www.mathworks.com/matlabcentral/newsreader/view_thread/238109). Apparently, the "out of memory" may not be due to the `364000000:628000000` array, but due to the fact that the entire `Z` is copied, at least in the first case, although I'm not sure if that's true for my 1-D case. – gerrit Oct 28 '13 at 19:24
  • Plus, my aim is not what's fast, but what's memory-efficient. Some of the methods proposed in those threads have the *advantage* that they're fast, but the *disadvantage* that it doesn't free up any memory... – gerrit Oct 28 '13 at 19:29
  • @gerrit - No, that link provided by natan refers to truncating rows, which is _very+ different than a 1D vector. For that link: "What you have above is truncating rows, which will necessitate data copying." That makes sense because when truncating rows, the data must remain contiguous in memory so a copy must take place. This is not the case here. – chappjc Oct 29 '13 at 01:01
  • I am not sure and don't have access to Matlab to check, but I think [] is shorthand for double.empty and you may be changing the class of Z. Have you tried single.empty instead? – StrongBad Oct 29 '13 at 19:13
  • @DanielE.Shub I quickly tested, and 'Z(N:end) = []` does not appear to change the class. I didn't know about the `empty` class method though, that's quite nice! (For future visitors: [Matlab docs on empty](http://www.mathworks.se/help/matlab/matlab_oop/creating-object-arrays.html?s_tid=doc_12b#brd4nrh), and see [this related question](http://stackoverflow.com/a/2594449/974555).) – gerrit Oct 29 '13 at 23:30

1 Answers1

15

I ran both examples on a machine with 24GB of RAM with profile('-memory','on');. This profiler option will show memory allocated and freed on each line of code. These are supposed to be gross not net amounts. I checked with a simple function that has net 0 free and alloc and it reported the gross amounts. However, it seems likely that builtin commands with no .m code to back them do not give fine-grained memory reporting to the profiler.

I ran a couple tests for the following code:

% truncTest.m
N = 628000000;
M = 364000000;

clear Z
Z = zeros(N,1,'single');
Z(M:end) = [];
Z(1) % just because

clear Z
Z = zeros(N,1,'single');
Z = Z(1:M);
Z(1)

For what they are worth, the memory profiling results for this N and M are:

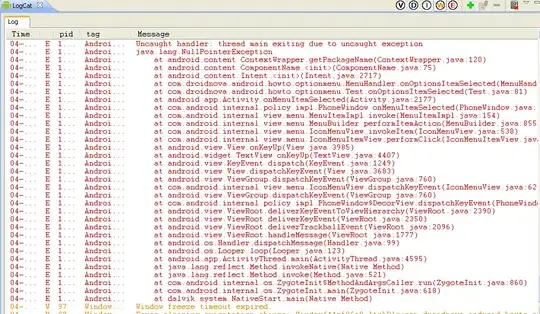
enter image description here

Well, both lines look the same in terms of memory allocated and freed. Maybe that's not the whole truth.

So, out of curiosity I decreased M to 200 (just 200!) without changing N, did profile clear and reran. Profiling claims:

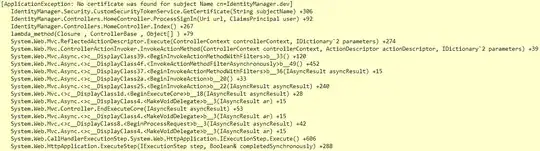
enter image description here

Interestingly, Z=Z(1:M); is practically instantaneous now, and Z(M:end)=[]; is a little faster. Both free about 2.4GB of memory, as expected.

Finally, if we go the other direction and set M=600000000;:

enter image description here

Now even Z=Z(1:M); is slow, but about twice as fast as Z(M:end)=[];.

This suggests:

  1. Z=Z(1:M); just grabs the indicated elements, stores them in a new buffer or temporary variable, releases the old buffer and assigns the new/temporary to the array Z. I was able to make my weaker 4GB machine go from 2.45 seconds to thrashing the page file for 5 minutes just by increasing M and leaving N alone. Definitely prefer this option for small M/N, probably in all cases.
  2. Z(M:end)=[]; always rewrites the buffer, and execution time increases with M too. Actually always slower, and seems to increase exponentially, unlike Z=Z(1:M);.
  3. Memory profiling does not give fine-grained information about these builtin operations and should not be misinterpreted as giving a total of memory freed and allocated over the commands execution, but rather a net change.

UPDATE 1: Just for fun I timed the tests at a range of values of M:

enter image description here

Clearly more informative than the profiling. Both methods are not no-ops, but Z=Z(1:M); is fastest, but it can use almost double the memory of Z for M/N near 1.

UPDATE 2:

A relatively unknown feature called mtic (and mtoc) were available in 32-bit Windows prior to R2008b. I still have it installed on one machine, so I decided to see if that provides any more insight, with the understanding that (a) much has changed since then and (b) it's a completely different memory manager used in 32-bit MATLAB. Still, I reduced the test size to N=128000000; M=101000000; and had a look. First, feature mtic for Z=Z(1:M-1);

>> tic; feature mtic; Z=Z(1:M-1); feature mtoc, toc

ans = 

      TotalAllocated: 808011592
          TotalFreed: 916009628
    LargestAllocated: 403999996
           NumAllocs: 86
            NumFrees: 77
                Peak: 808002024

Elapsed time is 0.951283 seconds.

Clearing up, recreating Z, the other way:

>> tic; feature mtic; Z(M:end) = []; feature mtoc, toc

ans = 

      TotalAllocated: 1428019588
          TotalFreed: 1536018372
    LargestAllocated: 512000000
           NumAllocs: 164
            NumFrees: 157
                Peak: 1320001404

Elapsed time is 4.533953 seconds.

In every metric (TotalAllocated, TotalFreed, NumAllocs, etc.), Z(M:end) = []; is less efficient than Z=Z(1:M-1);. I expect it is possible to discern what is going on in memory by examining these numbers for these values of N and M, but we'd be guessing about an old MATLAB

chappjc
  • 30,359
  • 6
  • 75
  • 132
  • A very interesting research. So, is there a matlab command that **efficiently** de-allocates part of an array? – Shai Oct 29 '13 at 05:36
  • @Shai - I would say the only good answer involves [`mxRealloc`](http://www.mathworks.com/help/matlab/apiref/mxrealloc.html), `mexMakeMemoryPersistent` and friends to do unsupported in-place array modification, but that's a longer answer. I think the tests here show these MATLAB expressions are not very efficient except in certain circumstances. – chappjc Oct 29 '13 at 05:39
  • 1
    @Shai - Note that the fast MEX solution identified in this [MATLAB newsreader](http://www.mathworks.com/matlabcentral/newsreader/view_thread/245581#631580) thread is rather silly from a memory efficiency point of view, since it doesn't actually free up any memory, as pointed out by gerrit. So it would have to be something more sophisticated... but I have to think that MathWorks can do better than us. :) – chappjc Oct 29 '13 at 06:00
  • Interesting, and I've learned that I really should always choose `Z = Z(1:M-1);` over `Z(M:end) = [];`. But the memory issue that I experienced seems not to be identified by the profiler, not even by the *peak memory* column, so it appears we can't really answer my core question, or can we? And, why is `Z = zeros(N,1,'single');` not shown in the profiler? – gerrit Oct 29 '13 at 10:54
  • @gerrit - That's correct, the profiler is only useful for peak and freed, and for expressions comprising built-in MALTAB commands it only seems to provide net values. The peak value seems useless here. The `zeros` line is not shown because those are only the lines were _most_ of the is spent (note the "All other lines" row). Scrolling down in the profiler you get a line-by-line summary. – chappjc Oct 29 '13 at 14:14
  • @chappjc Is allocating a 628000000-element array *and* filling it with zeroes, then, faster than deallocating one (`clear`, which *is* listed in the profiler)? – gerrit Oct 29 '13 at 14:34
  • @gerrit - I updated the answer again with another analysis that is perhaps more revealing, although for an older MATLAB version. The `clear` vs. initialization thing seems to be an issue of temporal resolution. I tried timing this again, and now I'm seeing that `clear` is way faster, but on a different MATLAB version... either way, these are minor lines that are both very fast compared to the truncation. – chappjc Oct 29 '13 at 15:19
  • @chappjc Great job! +1 I just found out about it through your profile – Luis Mendo May 09 '14 at 07:27
  • Your profile led me to this post as well. +1 for being a MATLAB boss. – rayryeng May 15 '14 at 16:22