1

I keep reading that searching is faster in ArrayList, as it is index based, in comparison with some other data structure like LinkedList. I understand that an ArrayList internally uses a Java array. Here is the code from Java's ArrayList that holds that data in an array.

private transient Object[] elementData;

What is 'index based data structure' and why is it faster?

Also, what is the memory model (how the array is structured in stack/heap combination) of an array so that I can understand why accessing an element in an array is faster?

Rakesh KR
  • 6,357
  • 5
  • 40
  • 55
PhantomReference
  • 718
  • 2
  • 14
  • 27
  • `arr[7] = 'foo';`. There. Index-based access. – Marc B Nov 25 '13 at 17:02
  • An ArrayList is backed by an Array, and the JVM optimizes array access. In contrast, a linked-list doesn't have an array backing it. – Elliott Frisch Nov 25 '13 at 17:03
  • Follow this http://stackoverflow.com/questions/716597/array-or-list-in-java-which-is-faster – Aditya Peshave Nov 25 '13 at 17:05
  • say you wanted the third element of a 0 based index structure...arr[2] = "theThirdElemnt"...this is much faster than say a linked list where you have to say head.next.next and repeat .next numerous times until you hit the correct node. Sometimes you may have to traverse O(n) to hit your element. Index based for search is O(1) – Josh Engelsma Nov 25 '13 at 17:05
  • 1
    It might be helpful to learn about arrays in something more low-level, like C, where array access is just arithmetic on a pointer (i.e. if the array starts at address `0x1000`, element 0 is at `ox1000 + (element_size * 0)`, element 1 is at `0x1000 + (element_size * 1)`, etc.). In Java it gets a bit more complicated because it introduces bounds checking, memory management, etc. and doesn't expose pointers to the user. – Mark Peters Nov 25 '13 at 17:06
  • Thank Marc B. My question was more like what makes an index based access faster. What goes on under the hood that explains the speed (may be the answer is related to the way in which an array is laid out in the memory that makes the index based access faster). – PhantomReference Nov 25 '13 at 17:06

3 Answers3

6

ArrayList is backed by an array. Typically, addressing something by index is assumed to be O(1), i.e., in constant time. In assembly, you can index into a memory location in constant time, as there are certain LOAD instructions that take an optional index in addition to a base address. Arrays are usually allocated in memory in a contiguous block. For example, assume you have a base address of 0x1000 (where the array starts) and you provide an index of 0x08. This means that for your array starting at 0x1000 you want to access the element at location 0x1008. The processor only needs to add the base address and the index, and look up that location in memory*. This can happen in constant time. So assume you have the following in Java:

int a = myArray[9];

Internally, the JVM will know the address of myArray. Like our example, let us assume that it is at location 0x1000. Then it knows that it needs to find the 9th subscript. So basically the location it needs to find is simply:

0x1000 + 0x09

Which gives us:

0x1009

So the machine can simply load it from there.

In C, this is actually a lot more evident. If you have an array, you can access the ith location as myArray[i] like in Java. But you can access it via pointer arithmetic too (a pointer contains an address of the actual value the pointer points to)! So if you had a pointer *ptrMyArray, you can access the ith subscript by doing *(ptrMyArray + i), which is exactly as I described: base address plus subscript!

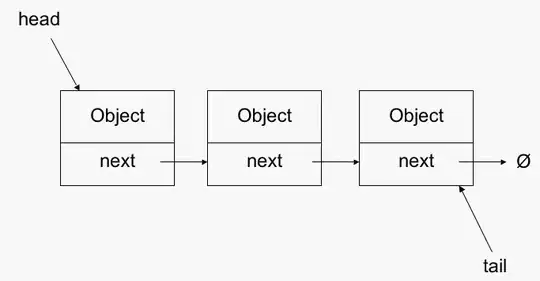
In contrast, the worst case for accessing a location in a LinkedList is O(n). If you recall your data structures, a linked list usually has a head and a tail pointer, and each node has a next pointer to the next node. So to find a node, you have to start with head and then inspect each node in turn until you get to the right one. You cannot simply index into a location either since there is no guarantee that the nodes of the linked list are next to each other in memory; they could be anywhere.

*Indexing must also take into account the size of the element, since you have to take into account how much space each element is taking. The basic example I provided assumes that each element only takes up a byte. But if you have larger elements, the formula is basically BASE_ADDRESS + (ELEMENT_SIZE_IN_BYTES * INDEX). In our case, where we assume a size of 1 byte, the formula reduces to BASE_ADDRESS + INDEX.

Vivin Paliath
  • 94,126
  • 40
  • 223
  • 295
  • 1
    +1, this is exactly what I wanted to understand. Thank you! Question: When you said 0x08, it roughly translates to something like Object o = arr[8]; in the code right? – PhantomReference Nov 25 '13 at 17:12
1

I don't know the exact internals of the JVM, and this might vary from VM to VM, but basically, an array is a contiguous block of slots in memory.

So, accessing array[1000] simply consists in getting the address of the array in memory, adding 1000 to it, and get the value stored at this location.

With a linked list, you have to get the address of the first node, then get the object referenced by this reference, then get the address of the second node, etc. until the 1000th element, which makes it a lot slower. And there is less chance of the whole thing to be stored in cache as well.

JB Nizet
  • 678,734
  • 91
  • 1,224
  • 1,255
0

Take a look Figure 3 from here and then you could compare it to a linked list from here. A Character Array A Linked List

Community
  • 1
  • 1
Elliott Frisch
  • 198,278
  • 20
  • 158
  • 249