I'm trying to understand the function lmer. I've found plenty of information about how to use the command, but not much about what it's actually doing (save for some cryptic comments here: http://www.bioconductor.org/help/course-materials/2008/PHSIntro/lme4Intro-handout-6.pdf). I'm playing with the following simple example:
library(data.table)
library(lme4)
options(digits=15)
n<-1000
m<-100
data<-data.table(id=sample(1:m,n,replace=T),key="id")
b<-rnorm(m)
data$y<-rand[data$id]+rnorm(n)*0.1
fitted<-lmer(b~(1|id),data=data,verbose=T)
fitted
I understand that lmer is fitting a model of the form Y_{ij} = beta + B_i + epsilon_{ij}, where epsilon_{ij} and B_i are independent normals with variances sigma^2 and tau^2 respectively. If theta = tau/sigma is fixed, I computed the estimate for beta with the correct mean and minimum variance to be
c = sum_{i,j} alpha_i y_{ij}
where
alpha_i = lambda/(1 + theta^2 n_i)
lambda = 1/[\sum_i n_i/(1+theta^2 n_i)]
n_i = number of observations from group i
I also computed the following unbiased estimate for sigma^2:
s^2 = \sum_{i,j} alpha_i (y_{ij} - c)^2 / (1 + theta^2 - lambda)
These estimates seem to agree with what lmer produces. However, I can't figure out how log likelihood is defined in this context. I calculated the probability density to be
pd(Y_{ij}=y_{ij}) = \prod_{i,j}[f_sigma(y_{ij}-ybar_i)]
* prod_i[f_{sqrt(sigma^2/n_i+tau^2)}(ybar_i-beta) sigma sqrt(2 pi/n_i)]
where
ybar_i = \sum_j y_{ij}/n_i (the mean of observations in group i)
f_sigma(x) = 1/(sqrt{2 pi}sigma) exp(-x^2/(2 sigma)) (normal density with sd sigma)
But log of the above is not what lmer produces. How is log likelihood computed in this case (and for bonus marks, why)?
Edit: Changed notation for consistency, striked out incorrect formula for standard deviation estimate.
 , where
, where  and
and 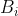 are independent normals with variances
are independent normals with variances  and
and 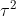 respectively. The joint probability distribution of
respectively. The joint probability distribution of 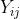 and
and 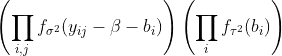
 .
.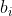 (which isn't observed) to give
(which isn't observed) to give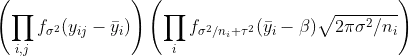
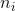 is the number of observations from group
is the number of observations from group 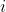 , and
, and 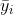 is the mean of observations from group
is the mean of observations from group 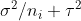 is the variance of
is the variance of 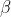 to give
to give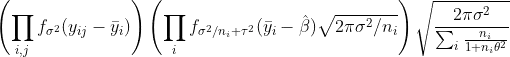
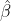 is given below.
is given below.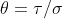 is fixed, we can explicitly find the
is fixed, we can explicitly find the  which maximise likelihood. They turn out to be
which maximise likelihood. They turn out to be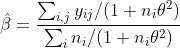
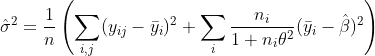
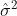 has two terms for variation within and between groups, and
has two terms for variation within and between groups, and 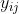 and the mean of
and the mean of 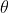 .
. in terms of
in terms of 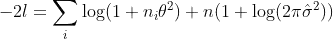
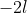 and
and 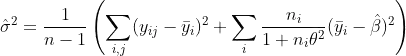
 is given by
is given by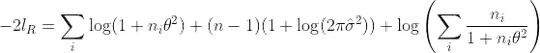
 and
and