Compare two bounding boxes with each other Matlab

Question

I have two the co-ordinates of two bounding boxes, one of them is the groundtruth and the other is the result of my work. I want to evaluate the accuracy of mine against the groundtruth one. So I'm asking if anyone has any suggestions

The bounding box details is saved in this format [x,y,width,height]

Answer 1

Edit: I have corrected the mistake pointed by other users.

I am assuming you are detecting some object and you are drawing a bounding box around it. This comes under widely studied/researched area of object detection. The best method of evaluating the accuracy will be calculating intersection over union. This is taken from the PASCAL VOC challenge, from here. See here for visuals.

If you have a bounding box detection and a ground truth bounding box, then the area of overlap between them should be greater than or equal to 50%. Suppose the ground truth bounding box is gt=[x_g,y_g,width_g,height_g] and the predicted bounding box is pr=[x_p,y_p,width_p,height_p] then the area of overlap can be calculated using the formula:

intersectionArea = rectint(gt,pr); %If you don't have this function then write a simple one for yourself which calculates area of intersection of two rectangles.
unionArea = (width_g*height_g)+(width_p*height_p)-intersectionArea;
overlapArea = intersectionArea/unionArea; %This should be greater than 0.5 to consider it as a valid detection.

I hope its clear for you now.

Answer 2

Try intersection over Union

Intersection over Union is an evaluation metric used to measure the accuracy of an object detector on a particular dataset.

More formally, in order to apply Intersection over Union to evaluate an (arbitrary) object detector we need:

1. The ground-truth bounding boxes (i.e., the hand labeled bounding boxes from the testing set that specify where in the image our object is).
2. The predicted bounding boxes from our model.

Below I have included a visual example of a ground-truth bounding box versus a predicted bounding box:

The predicted bounding box is drawn in red while the ground-truth (i.e., hand labeled) bounding box is drawn in green.

In the figure above we can see that our object detector has detected the presence of a stop sign in an image.

Computing Intersection over Union can therefore be determined via:

As long as we have these two sets of bounding boxes we can apply Intersection over Union.

Here is the Python code

# import the necessary packages
from collections import namedtuple
import numpy as np
import cv2

# define the `Detection` object
Detection = namedtuple("Detection", ["image_path", "gt", "pred"])

def bb_intersection_over_union(boxA, boxB):
    # determine the (x, y)-coordinates of the intersection rectangle
    xA = max(boxA[0], boxB[0])
    yA = max(boxA[1], boxB[1])
    xB = min(boxA[2], boxB[2])
    yB = min(boxA[3], boxB[3])

    # compute the area of intersection rectangle
    interArea = (xB - xA + 1) * (yB - yA + 1)

    # compute the area of both the prediction and ground-truth
    # rectangles
    boxAArea = (boxA[2] - boxA[0] + 1) * (boxA[3] - boxA[1] + 1)
    boxBArea = (boxB[2] - boxB[0] + 1) * (boxB[3] - boxB[1] + 1)

    # compute the intersection over union by taking the intersection
    # area and dividing it by the sum of prediction + ground-truth
    # areas - the interesection area
    iou = interArea / float(boxAArea + boxBArea - interArea)

    # return the intersection over union value
    return iou

The gt and pred are

1. gt : The ground-truth bounding box.
2. pred : The predicted bounding box from our model.

For more information, you can click this post

Answer 3

You should compute intersection and union, then the Jaccard index (intersection/union) is a value between 0 and 1 (1 mean perfect match, 0 mean perfect mismatch).

Answer 4

The answer that has been marked best answer above is wrong.

The solution suggested by @Parag actually calculates the ratio of intersection area and area of the minimum covering rectangle. It should be the union area instead.

So, the code would be

rect1 = [x1,y1,w1,h1]; 
rect2 = [x2,y2,w2,h2];
intersectionArea = rectint(rect1,rect2);
unionArea = w1*h1 + w2*h2 - intersectionArea;
overlap = intersectionArea/unionArea;

You can check this code to confirm the above (This code won the Pascal challenge).

Answer 5

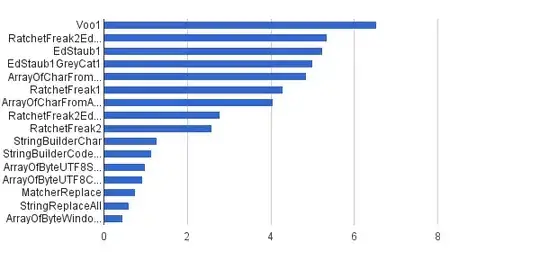
All answers to the question suggest using intersection over union (IoU) metric. This is a vectorized version of IoU that can be used for multiple roi matching.

function [IoU, match] = rectIoU(R1, R2, treshold)
I = rectint(R1, R2);
A1 = R1(:, 3).*R1(:, 4);
A2 = R2(:, 3).*R2(:, 4);
U = bsxfun(@plus, A1, A2')-I;
IoU = I./U;
if nargout > 1
    if nargin<3
        treshold = 0.5;
    end
    match = IoU>treshold;
end
end

It calculates pairwise IoU for two sets of bounding boxes. If R1 and R2 each specify one rectangle, the output IoU is a scalar.

R1 and R2 can also be matrices, where each row is a position vector ([x y w h]). IoU is then a matrix giving the IoU of all rectangles specified by R1 with all the rectangles specified by R2. That is, if R1 is n-by-4 and R2 is m-by-4, then IoU is an n-by-m matrix where IoU(i,j) is the IoU of the rectangles specified by the ith row of R1 and the jth row of R2.

It also accepts a scalar parameter, treshold, to set the match output. Size of match is exactly like IoU. match(i,j) indicates if the rectangles specified by the ith row of R1 and the jth row of R2 match.

For example,

R1 = [0 0 1 1; 2 1 1 1];
R2 = [-.5 2 1 1; flipud(R1)];
R2 = R2+rand(size(R2))*.4-.2;
[IoU, match] = rectIoU(R1, R2, 0.4)

returns:

IoU =
     0         0    0.7738
     0    0.6596         0


match =
     0     0     1
     0     1     0

that means R1(1, :) and R1(2, :) match R2(3, :) and R2(2, :) respectively.

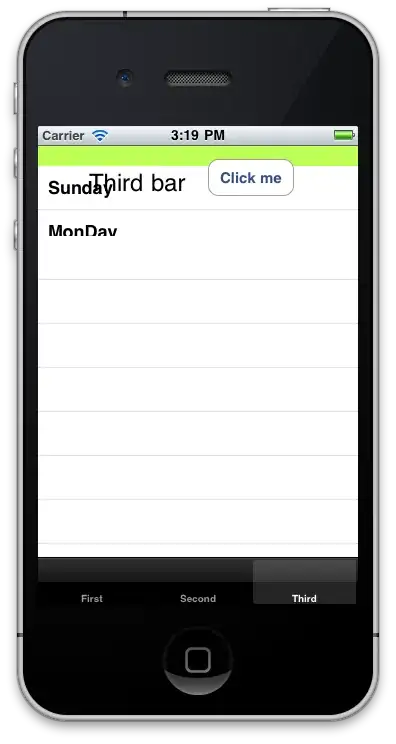
PS: At the time I'm posting this answer, there is a small mistake in Parag's answer (the accepted answer above). IMHO they calculate the union area in a wrong way. The unionCoords in their answer is actually the blue square in the picture below, and unionArea is its area, that obviously is not the union area of red and green rectangles.

Answer 6

Just an extension to what @Parag S. Chandakkar said. I have edited his code to get overlap ratio matrix for many number of boxes.

Incase you have you want to build function and directly use it to get overlap matrix (M,N) (each entry lies between [0,1]) for Box1(M,4) and Box2(N,4). (Box1 and Box2 contains(x,y,width,height) data of M and N boxes respectively).

    function result= overlap_matrix(box1,box2)
    [m,y1]=size(box1);
    [n,y2]=size(box2);
    result=zeros(m,n,'double');
    for  i = 1:m 
      for j=1:n
         gt=box1(i,:);
         pr=box2(j,:);

         x_g=box1(i,1);
         y_g=box1(i,2);
         width_g=box1(i,3);
         height_g=box1(i,4);

         x_p=box2(j,1);
         y_p=box2(j,2);
         width_p=box2(j,3);
         height_p=box2(j,4);
         intersectionArea=rectint(gt,pr); 
         unionCoords=[min(x_g,x_p),min(y_g,y_p),max(x_g+width_g-1,x_p+width_p-1),max(y_g+height_g-1,y_p+height_p-1)];
         unionArea=(unionCoords(3)-unionCoords(1)+1)*(unionCoords(4)-unionCoords(2)+1);
         overlapArea=intersectionArea/unionArea; 
         result(i,j)=overlapArea;
      end
    end

This is kindof parallel function to bboxOverlapRatio (http://in.mathworks.com/help/vision/ref/bboxoverlapratio.html) but not available in R2014a or earlier.