Okay so I have this project I have to do, but I just don't understand it. The thing is, I have 2 algorithms. O(n^2) and O(n*log2n).
Anyway, I find out in the project info that if n<100, then O(n^2) is more efficient, but if n>=100, then O(n*log2n) is more efficient. I'm suppose to demonstrate with an example using numbers and words or drawing a photo. But the thing is, I don't understand this and I don't know how to demonstrate this.
Anyone here that can help me understand how this works?
Good question. Actually, I always show these 3 pictures:
So, O(N*log(N)) is far better than O(N^2). It is much closer to O(N) than to O(N^2).
But your O(N^2) algorithm is faster for N < 100 in real life. There are a lot of reasons why it can be faster. Maybe due to better memory allocation or other "non-algorithmic" effects. Maybe O(N*log(N)) algorithm requires some data preparation phase or O(N^2) iterations are shorter. Anyway, Big-O notation is only appropriate in case of large enough Ns.
If you want to demonstrate why one algorithm is faster for small Ns, you can measure execution time of 1 iteration and constant overhead for both algorithms, then use them to correct theoretical plot:
Or just measure execution time of both algorithms for different Ns and plot empirical data.
Just ask wolframalpha if you have doubts.
In this case, it says
n log(n)
lim --------- = 0
n^2
Or you can also calculate the limit yourself:
n log(n) log(n) (Hôpital) 1/n 1
lim --------- = lim -------- = lim ------- = lim --- = 0
n^2 n 1 n
That means n^2 grows faster, so n log(n) is smaller (better), when n is high enough.
Big-O notation is a notation of asymptotic complexity. This means it calculates the complexity when N is arbitrarily large.
For small Ns, a lot of other factors come in. It's possible that an algorithm has O(n^2) loop iterations, but each iteration is very short, while another algorithm has O(n) iterations with very long iterations. With large Ns, the linear algorithm will be faster. With small Ns, the quadratic algorithm will be faster.
So, for small Ns, just measure the two and see which one is faster. No need to go into asymptotic complexity.
Incidentally, don't write the basis of the log. Big-O notation ignores constants - O(17 * N) is the same as O(N). Since log2N is just ln N / ln 2, the basis of the logarithm is just another constant and is ignored.
Let's compare them,
On one hand we have:
n^2 = n * n
On the other hand we have:
nlogn = n * log(n)
Putting them side to side:
n * n versus n * log(n)
Let's divide by n which is a common term, to get:
n versus log(n)
Let's compare values:
n = 10 log(n) ~ 2.3
n = 100 log(n) ~ 4.6
n = 1,000 log(n) ~ 6.9
n = 10,000 log(n) ~ 9.21
n = 100,000 log(n) ~ 11.5
n = 1,000,000 log(n) ~ 13.8
So we have:
n >> log(n) for n > 1
n^2 >> n log(n) for n > 1
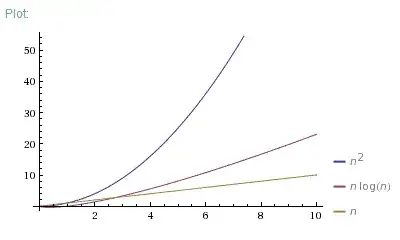
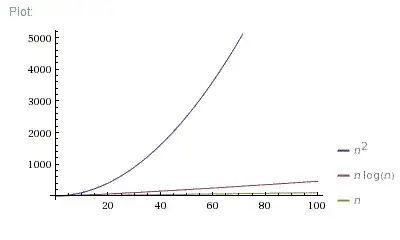
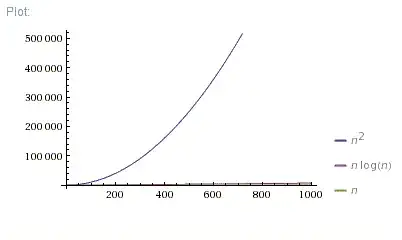
Anyway, I find out in the project info that if n<100, then O(n^2) is more efficient, but if n>=100, then O(n*log2n) is more efficient.
Let us start by clarifying what is Big O notation in the current context. From (source) one can read:
Big O notation is a mathematical notation that describes the limiting behavior of a function when the argument tends towards a particular value or infinity. (..) In computer science, big O notation is used to classify algorithms according to how their run time or space requirements grow as the input size grows.
Big O notation does not represent a function but rather a set of functions with a certain asymptotic upper-bound; as one can read from source:
Big O notation characterizes functions according to their growth rates: different functions with the same growth rate may be represented using the same
Onotation.
Informally, in computer-science time-complexity and space-complexity theories, one can think of the Big O notation as a categorization of algorithms with a certain worst-case scenario concerning time and space, respectively. For instance, O(n):
An algorithm is said to take linear time/space, or O(n) time/space, if its time/space complexity is O(n). Informally, this means that the running time/space increases at most linearly with the size of the input (source).
and O(n log n) as:
An algorithm is said to run in quasilinear time/space if T(n) = O(n log^k n) for some positive constant k; linearithmic time/space is the case k = 1 (source).
Mathematically speaking the statement
Which is better: O(n log n) or O(n^2)
is not accurate, since as mentioned before Big O notation represents a set of functions. Hence, more accurate would have been "does O(n log n) contains O(n^2)". Nonetheless, typically such relaxed phrasing is normally used to quantify (for the worst-case scenario) how a set of algorithms behaves compared with another set of algorithms regarding the increase of their input sizes. To compare two classes of algorithms (e.g., O(n log n) and O(n^2)) instead of
Anyway, I find out in the project info that if n<100, then O(n^2) is more efficient, but if n>=100, then O(n*log2n) is more efficient.
you should analyze how both classes of algorithms behaves with the increase of their input size (i.e., n) for the worse-case scenario; analyzing n when it tends to the infinity
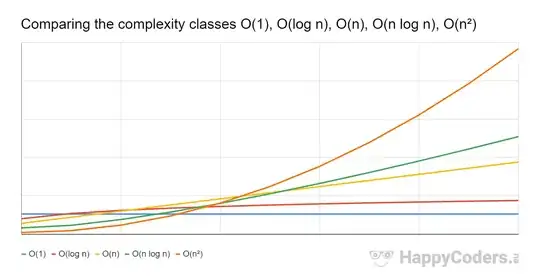
As @cem rightly point it out, in the image "big-O denote one of the asymptotically least upper-bounds of the plotted functions, and does not refer to the sets O(f(n))"
As you can see in the image after a certain input, O(n log n) (green line) grows slower than O(n^2) (orange line). That is why (for the worst-case) O(n log n) is more desirable than O(n^2) because one can increase the input size, and the growth rate will increase slower with the former than with the latter.
First, it is not quite correct to compare asymptotic complexity mixed with N constraint. I.E., I can state:
O(n^2) is slower than O(n * log(n)), because the definition of Big O notation will include n is growing infinitely.
For particular N it is possible to say which algorithm is faster by simply comparing N^2 * ALGORITHM_CONSTANT and N * log(N) * ALGORITHM_CONSTANT, where ALGORITHM_CONSTANT depends on the algorithm. For example, if we traverse array twice to do our job, asymptotic complexity will be O(N) and ALGORITHM_CONSTANT will be 2.
Also I'd like to mention that O(N * log2N) which I assume logariphm on basis 2 (log2N) is actually the same as O(N * log(N)) because of logariphm properties.
We have two way to compare two Algo ->first way is very simple compare and apply limit
T1(n)-Algo1
T2(n)=Alog2
lim (n->infinite) T1(n)/T2(n)=m
(i)if m=0 Algo1 is faster than Algo2
(ii)m=k Both are same
(iii)m=infinite Algo2 is faster
*Second way pretty simple as compare to 1st there you just take a log of both but do not neglet multi constant
Algo 1=log n
Algo 2=sqr(n)
keep log n =x
Any poly>its log
O(sqr(n))>o(logn)
I am a mathematician so i will try to explain why n^2 is faster than nlogn for small values of n , with a simple limit , while n-->0 :
lim n^2 / nlogn = lim n / logn = 0 / -inf = 0
so , for small values of n ( in this case "small value" is n existing in [1,99] ) , the nlogn is faster than n^2 , 'cause as we see limit = 0 . But why n-->0? Because n in an algorithm can take "big" values , so when n<100 , it is considered like a very small value so we can take the limit n-->0.
