3

pic

I am trying to work this out in java with LatLng point

I was looking at this post here Circle line-segment collision detection algorithm?

I have a method to find distance between 2 point. The instruction says

Project the vector AC onto AB. The projected vector, AD, gives the new point D. If the distance between D and C is smaller than (or equal to) R we have an intersection.

I don't have knowledge about vector, could anyone help me how to find point D here ?

Thanks in advance

Community
  • 1
  • 1
JustWe
  • 633
  • 1
  • 5
  • 18
  • 1
    Well, if the co-ordinates of `A` are `(ax,ay)`, and similarly for `B, C, D`, then the length of line segment `CD` is `|(cy-ay)(bx-ax)-(cx-ax)(by-ay)|/sqrt((bx-ax)^2+(by-ay)^2)` - I'll write a proper answer with a proof if I have time later. Or you could take it to math.stackexchange.com, where the experts in this kind of thing hang out. – Dawood ibn Kareem May 21 '14 at 02:38
  • thanks for the quick reply, in the meantime, I will try implement that as well. – JustWe May 21 '14 at 02:45
  • Problem still remain. I am still looking for a way to find point D – JustWe May 21 '14 at 03:44
  • D= A + AC*cos(angle). I think that angle is 30 degree => D = A + AC/2 – Arnaldo Ignacio Gaspar Véjar May 21 '14 at 03:55
  • I thought you just wanted to know whether the length of CD was more or less than R. Why do you need to know the coordinates of D? – Dawood ibn Kareem May 21 '14 at 03:55
  • @ArnaldoIgnacioGasparVéjar - not only is there no reason to assume that the angle is 30 degrees, but also `cos(30 degrees)` is not `1/2`. – Dawood ibn Kareem May 21 '14 at 03:56
  • @David Wallace its another point in this calculation I need to know as well to use it in the future. Sorry for unclear question. But I also stated to find point D in the question as well – JustWe May 21 '14 at 03:58
  • True, you did. OK, as I said, I will post an answer later if I have time. – Dawood ibn Kareem May 21 '14 at 04:07

2 Answers2

2

If you really need D point coordinates - let's vectors
AB = (B.X-A.X, B.Y-A.Y)
AC = (C.X-A.X, C.Y-A.Y)
then the simplest (I believe) form of projection of C to AB is:

AD = AB * (AB.dot.AC) / (AB.dot.AB);
In coordinates:

CF=((B.X-A.X)*(C.X-A.X)+(B.Y-A.Y)*(C.Y-A.Y))/((B.X-A.X)^2+(B.Y-A.Y)^2)
D.X=A.X+(B.X-A.X)*CF
D.Y=A.Y+(B.Y-A.Y)*CF

Distance CD, as David Wallace has already written, is
|CD| = |AC x AB|/|AB| (x = cross product)

MBo
  • 77,366
  • 5
  • 53
  • 86
  • thanks, I will try to verify that, but it might take sometime to test it for me, therefore, answer vote will be slow – JustWe May 21 '14 at 04:40
  • What is CF variable? – Petr Jun 02 '19 at 19:33
  • CF is dimensionless parameter in vector equation `AD = cf * AB`(it is proportional to cosine of angle CAB and AC length) – MBo Jun 03 '19 at 04:06
0

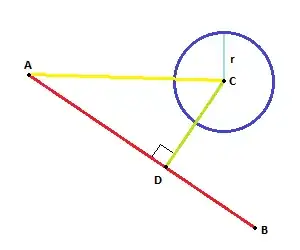
Let's think of A, B, C and D as Vectors and let

* for 2 vectors be the scalar product, i.e. the result is the sum of the products of the corresponding coordinates of the operands, and

|X| be the length of vector x, i.e. the square root of the sum of the squared values of the coordiantes of X

First we find the plane P (for 2D space the plane is a line) ortogonal to F = (B-A), that contains C:

This plane is described by the following equation (where Z is arbitrary point in the plane):

F * Z = F * C

The equation for the line G from A to B is (tin real numbers):

F * t + A

To intersect P and G you have to solve the following equation:

  (F * t + A) * F = F * C
t * |F|^2 + A * F = F * C
        t * |F|^2 = F * C - A * F
                t = (F * (C - A)) / (|F|^2)
                t = ((B - A) * (C - A)) / (|B-A|^2)

To get D insert t into G:

D = F * t + A
  = (B-A) * t + A

In a 2D space, you get

ca1 = C1-A1
ca2 = C2-A2
ba1 = B1-A1
ba2 = B2-A2
t   = (ba1 * ca1 + ba2 * ca2) / (ba1 * ba1 + ba2 * ba2) 


D1 = ba1 * t + A1
D2 = ba2 * t + A2

Where C1 and C2 are the coordinates of C, A1 and A2 are the coordinates of A, ect.

fabian
  • 80,457
  • 12
  • 86
  • 114