The information in the question about the model, suggest to specify fixed = y ~ 1 + x and random = ~ us(1 + x):cluster. With us() you allow the random effects to be correlated (cf. section 3.4 and table 2 in Hadfield's 2010 jstatsoft-article)
First of all, as you only have one dependent variable (y), the G part in the prior (cf. equation 4 and section 3.6 in Hadfield's 2010 jstatsoft-article) for the random effects variance(s) only needs to have one list element called G1. This list element isn't the actual prior distribution - this was specified by Hadfield to be an inverse-Wishart distribution. But with G1 you specify the parameters of this inverse-Whishart distribution which are the scale matrix (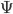 in Wikipedia notation and
in Wikipedia notation and V in MCMCglmm notation) and the degrees of freedom (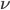 in Wikipedia notation and
in Wikipedia notation and nu in MCMCglmm notation). As you have two random effects (the intercept and the slope) V has to be a 2 x 2 matrix. A frequent choice is the two dimensional identity matrix diag(2). Hadfield often uses nu = 0.002 for the degrees of freedom (cf. his course notes)
Now, you also have to specify the R part in the prior for the residual variance. Here again an inverse-Whishart distribution was specified by Hadfield, leaving the user to specify its parameters. As we only have one residual variance, V has to be a scalar (lets say V = 0.5). An optional element for R is fix. With this element you specify, whether the residual variance shall be fixed to a certain value (than you have to write fix = TRUE or fix = 1) or not (then fix = FALSE or fix = 0). Notice, that you don't fix the residual variance to be 0.5 by fix = 0.5! So when you find in Hadfield's course notes fix = 1, read it as fix = TRUE and look to which value of V it is was fixed.
All togehter we set up the prior as follows:
prior0 <- list(G = list(G1 = list(V = diag(2), nu = 0.002)),
R = list(V = 0.5, nu = 0.002, fix = FALSE))
With this prior we can run MCMCglmm:
library("MCMCglmm") # for MCMCglmm()
set.seed(123)
mod0 <- MCMCglmm(fixed = y ~ 1 + x,
random = ~ us(1 + x):cluster,
data = dat,
family = "categorical",
prior = prior0)
The draws from the Gibbs-sampler for the fixed effects are found in mod0$Sol, the draws for the variance parameters in mod0$VCV.
Normally a binomial model requires the residual variance to be fixed, so we set the residual variance to be fixed at 0.5
set.seed(123)
prior1 <- list(G = list(G1 = list(V = diag(2), nu = 0.002)),
R = list(V = 0.5, nu = 0.002, fix = TRUE))
mod1 <- MCMCglmm(fixed = y ~ 1 + x,
random = ~ us(1 + x):cluster,
data = dat,
family = "categorical",
prior = prior1)
The difference can be seen by comparing mod0$VCV[, 5] to mod1$VCV[, 5]. In the later case, all entries are 0.5 as specified.
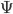 in Wikipedia notation and
in Wikipedia notation and 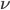 in Wikipedia notation and
in Wikipedia notation and