64

Given the function below: 

int f(int n) {
  if (n <= 1) {
    return 1;
  }
  return f(n - 1) + f(n - 1);
}

I know that the Big O time complexity is O(2^N), because each call calls the function twice.

What I don't understand is why the space/memory complexity is O(N)?

George Kagan
  • 5,913
  • 8
  • 46
  • 50

6 Answers6

93

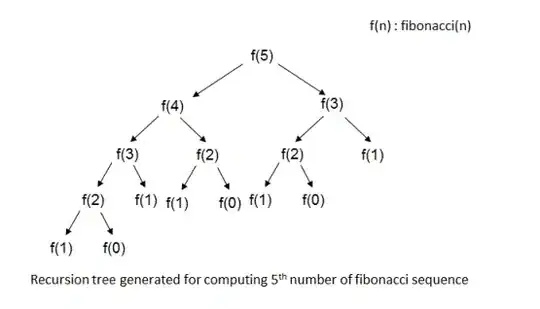
A useful way to approach these types of problems is by thinking of the recursion tree. The two features of a recursive function to identify are:

  1. The tree depth (how many total return statements will be executed until the base case)
  2. The tree breadth (how many total recursive function calls will be made)

Our recurrence relation for this case is T(n) = 2T(n-1). As you correctly noted the time complexity is O(2^n) but let's look at it in relation to our recurrence tree.

      C
     / \         
    /   \      
T(n-1)  T(n-1)

            C
       ____/ \____
      /           \
    C              C   
   /  \           /  \
  /    \         /    \
T(n-2) T(n-2) T(n-2)  T(n-2)

This pattern will continue until our base case which will look like the following image:

enter image description here

With each successive tree level, our n reduces by 1. Thus our tree will have a depth of n before it reaches the base case. Since each node has 2 branches and we have n total levels, our total number of nodes is 2^n making our time complexity O(2^n).

Our memory complexity is determined by the number of return statements because each function call will be stored on the program stack. To generalize, a recursive function's memory complexity is O(recursion depth). As our tree depth suggests, we will have n total return statements and thus the memory complexity is O(n).

Yassin Hajaj
  • 21,337
  • 9
  • 51
  • 89
Ritwik Biswas
  • 1,329
  • 1
  • 13
  • 18
  • 6
    https://stackoverflow.com/questions/33590205/how-do-you-find-the-space-complexity-of-recursive-functions-such-as-this-one this is much clearer – arielorvits Dec 12 '18 at 22:08
  • 2
    Quoting the key takeaway statement from this answer: "memory complexity is determined by the number of return statements because each function call will be stored on the program stack. To generalize, a recursive function's memory complexity is O(recursion depth). As our tree depth suggests, we will have n total return statements and thus the memory complexity is O(n)." But does that mean all recursive calls have O(n) space complexity? (Function always returns only once right?) – Akshay Lokur Mar 01 '21 at 17:11
13

Here's how I think about it:

  • The temptation is to say that the space complexity will also be O(2^N), because after all, memory has to be allocated for each of the O(2^N) recursive calls, right? (not right)
  • In actuality the values are added together/collapsed at each call and thus the space required will just be the result of each call starting at the base case on up, forming the array [f(1), f(2), f(3) ... f(n)], in other words just O(n) memory
Nic Scozzaro
  • 6,651
  • 3
  • 42
  • 46
2

I am find a clear answer in two articles.

First

At this article , it told me why the space complexity is O(n).

but i am also confuse for that why the stack frames only have f(5) -> f(4) -> f(3) -> f(2) -> f(1) but without f(5) -> f(4) -> f(3) -> f(2) -> f(0) and others at onece time.

The Fibonacci tree image:

enter image description here

then i finaly find a answer in the second article, it clear my confusing.

Second

At this article it's helpful. you can see the detail here.

The stack frames image: enter image description here

Thanks.

Jesse
  • 93
  • 6
0

This can be better explained considering a different function
f(n) = f(n-1) + f(n-2)
f(0) =0, f(1)=1

which would result in following tree of calculation for f(4)


      f(4)
   f(3)      f(2)
 f(2)   f(1)  f(1)  f(0)
f(1) f(0)


System can process the calculation with reduplicated storage stack equal to depth (storage unit for f(0), f(1), f(2), f(3) and f(4)). While runtime needs to account for all operations at each node (addition or return statement) - hence is a factor of none of the nodes.

ZF007
  • 3,708
  • 8
  • 29
  • 48
Redsha
  • 1
  • 1
0

Recursion Problem we can think like we are implementing with stack, so if the first function calls itself second function pause and it traverses through the end and added to the stack one by one and after finishing it will return and one by one remove from the topmost stack, and then second function resume and traverse through the end and adding to topmost of the stack and at returning time removes. But it uses the same stack and it will take at most n space under the same stack so space complexity is used O(n).

prashant sargar
  • 11
-1

Each call adds a level to the stack.

f(4)

f(3) f(2) f(1) f(0)

Each of these calls is added to the call stack and takes up actual memory. However, just because you have n calls total doesn't mean it takes O(n). So this would take O(n) space.

Rishabh Singh
  • 1
  • 2