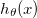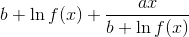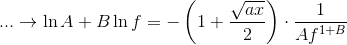Which f(x) minimizes the order of g(f(x)) as x goes to infinity

Question

Assume f(x) goes to infinity as x tends to infinity and a,b>0. Find the f(x) that yields the lowest order for

as x tends to infinity. By order I mean Big O and Little o notation.

I can only solve it roughly:

My solution: We can say ln(1+f(x)) is approximately equal to ln(f(x)) as x goes to infinity. Then, I have to minimize the order of

Since for any c>0, y+c/y is miminized when y =sqrt(c), b+ln f(x)}=sqrt(ax) is the anwer. Equivalently, f(x)=e^(sqrt(ax)-b) and the lowest order for g(x) is 2 sqrt(ax).

Can you help me obtain a rigorous answer?

Answer 1

The rigorous way to minimize (I should say extremize) a function of another function is to use the Euler-Lagrange relation:

Thus:

Taylor expansion:

If we only consider up to "constant" terms:

Which is of course the result you obtained.

---

Next, linear terms:

We can't solve this equation analytically; but we can explore the effect of a perturbation in the function f(x) (i.e. a small change in parameter to the previous solution). We can obviously ignore any linear changes to f, but we can add a positive multiplicative factor A:

sqrt(ax) and Af are obviously both positive, so the RHS has a negative sign. This means that ln(A) < 0, and thus A < 1, i.e. the new perturbed function gives a (slightly) tighter bound. Since the RHS must be vanishingly small (1/f), A must not be very much smaller than 1.

Going further, we can add another perturbation B to the exponent of f:

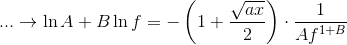
Since ln(A) and the RHS are both vanishing small, the B-term on LHS must be even smaller for the sign to be consistent.

So we can conclude that (1) A is very close to 1, (2) B is much smaller than 1, i.e. the result you obtained is in fact a very good upper bound.

The above also leads to the possibility of even tighter bounds for higher powers of f.