Ranking the best groupings of data based on past observed groupings

Question

Help me solve this problem:

I want to figure out how to group these animals.

Let's say everyday you observe one group of animals hanging out as friends. You want to figure out the best way to group the animals yourself depending on who they like best.

To illustrate, you observe:

Today, you saw these animals chilling out together: { Elephant Tiger Giraffe Peacock }

The next day you saw these: { Giraffe Peacock Elephant Lion Monkey }

And then the next day: { Elephant Tiger Hyena Rhino }

So from this you might conclude that the Elephant and the Tiger are good friends because they've hung out on two separate occasions. You would say the same for the Peacock and the Elephant.

What would be an algorithm for determining the best way to group these animals?

To give a little more detail, I'm working on a big data type problem and am trying to classify this problem.

Can machine learning solve this?

The real data might look more like this:

{A B F G R P K U J H} {A F G K B J H A S} And millions of lines of this...

Pointing me in the right direction would be helpful too.

Answer 1

There are various ways to approach this problem, but a simple formulation might be to design a scoring function for any given group of animals based on your data, and then perform a numerical optimization such as simulated annealing to find the partition of animals into groups that approximately maximizes your total score. Or if the number of animals is small enough you can just do an exhaustive search of all partitions.

You should choose your scoring function carefully ensure that you don't end up with n groups of size 1 or 1 group of size n. And don't forget to respect symmetry.

You could start by computing the probabilities of each pair of animals appearing together, then scale the set of all probabilities to have zero mean, and then score each group G as the sum of the pairwise scaled scores:

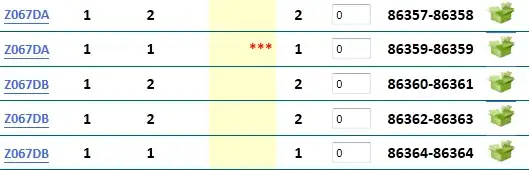
This is just a first try, you should be able to come up with better scoring functions.

Then to apply simulated annealing for k timesteps:

Choose a random partition π
for i = 0 to k:
    T = i/k #floating point division
    make a random transition to partition π'
    if P_accept(π, π', T) > rand(0,1):
        π <- π'
return π

Where a random transition is a swap of one animal from one group to another, including into a new empty group.

P_accept is the acceptance probability function you must design as described in the simulated annealing article. This should be based on the scores of two partitions and the temperature. The score of a partition could be the sum of the scores of each group in the partition, for example. For more info on designing an acceptance probability function see here.

Notice that you don't actually need an absolute score of a partition to run simulated annealing. You could do with a function that compares one partition to another. There are a few ways you might design such a function, but if you want to bring out the big guns you can consider using a Generalized Bradley Terry Model [pdf]. You can train on your input data to get a numerical parameter γ for each animal with the property that:

For example. This should give you a much better measure of group desirability, and it should fit much more nicely into the simulated annealing framework!