How do I avoid loss of precision with doubles in Java?

Question

I am writing a program that takes raw double values from a database and converts them to 8-byte hex strings, but I don't know how to prevent loss of precision. The data recieved from all devices are stored as doubles, including the 8-byte identification values.

Instances of doubles such as 7.2340172821234e+16 parse correctly without loss of precision, where the exponent is 10^16.

However, in instances where the exponent is 10^17, Java loses precision. For example, 2.88512954935019e+17 is interpreted by Java as 1.44464854248327008E17

The code I am using looks like this:

public Foo(double bar) {
    this.barString = Long.toHexString((long) bar);
    if (barString.length == 15) {
        barString = "0" + barString; //to account for leading zeroes lost on data entry
    }
}

I am using a test case similar to this to test it:

@Test
public void testFooConstructor() {
    OtherClass other = new OtherClass();
    
    OtherClass.Foo test0 = other.new Foo(72340172821234000d); //7.2340172821234e+16
    assertEquals("0101010100000150", test0.barString); //This test passes
    
    OtherClass.Foo test1 = other.new Foo(144464854248327000d);//1.44464854248327e+17
    assertEquals("02013e0500000758, test1.barString); //This test fails
}

The unit test states:

Expected: 02013e0500000758
Actual:   02013e0500000760

When I print out the values that Java stored 72340172821234000d and 144464854248327000d as it respectively prints:

7.2340172821234E16

1.44464854248327008E17

The latter value is off by 8, which seems to be consistent for the few that I have tested.

Is there anything I can do to correct this error?

EDIT: This is not a problem where I care about what is past the ones place. The question that some think this is a duplicate of is asking why floating point numbers are less precise, I am asking how to avoid the loss of precision, through similar workarounds to those that Roman Puchkovskiy suggested.

You cannot. `double` has limited precision. – Boris the Spider Aug 03 '17 at 19:08 — Boris the Spider, Aug 03 '17 at 19:08
@DwB Or, if it's an integer, BigInteger. – Bernhard Barker Aug 03 '17 at 19:54 — Bernhard Barker, Aug 03 '17 at 19:54

score 2 · Accepted Answer · edited Aug 04 '17 at 06:29

You could take your floating point values from database as strings (and not floating points) and then use BigDecimal to convert them to long:

String fpAsString = getFromDB();
long longValue = new BigDecimal(fpAsString).longValue();
this.barString = Long.toHexString(longValue);

BigDecimal.longValue() is analogous to narrowing primitive conversion from double to long, but it does not lose precision (apart from the loss of fractional part). You can lose something if the result does not fit into long, but the same will happen with your cast to long.

Ori Shalom · Answer 2 · 2017-08-03T20:06:30.460

Float and Double types are variables that very good for storing either very large numbers or very small numbers but very bad with storing numbers with large number of digits and this is due to their binary representation.

Basically if taking a look at how Double or Float are stored in the memory, there are one bit for the sign, several bits for the exponent and several bits for the fraction.

So when looking at how the value is actually stored in the memory it is something like this:

bits

And the actual value is calculated as follow:

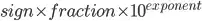
formula

(This example refer to Float which represented with 32 bits, Doubles is represented with 64 bits but the same principles apply)

The number of digits the number can represent is limited to the number of digits the fraction part can represent, but even with a very limited number of digits doubles and floats can represent very big numbers and very small numbers by using the exponent.

In java Double, the fraction part take 52 bits, if you will check in the calculator what is the biggest number a 52 bits number can be ( formula2 ) you will see you will get a 16 digits number. Double can represent bigger numbers than that by adding zeroes before or after using the number represented by the exponent, but it can't store number that have more than 16 digits without lose of precision.

Notice, there is actually more to it and this is only a very basic explanation to Double and Float representation. If you want to dive to the more accurate explanation you can check this wikipedia page: https://en.wikipedia.org/wiki/Single-precision_floating-point_format

How do I avoid loss of precision with doubles in Java?

2 Answers2