Get all coordinates points within known boundaries in a numpy matrix for each dot

Question

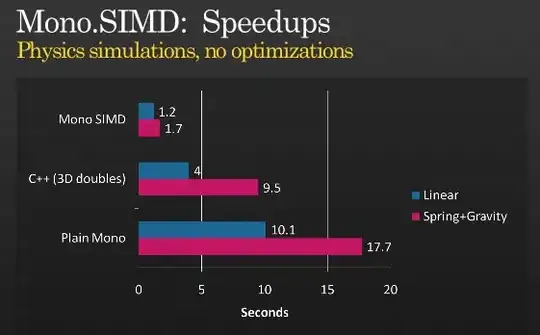
Given the following numpy matrix

import numpy as np

np_matrix = np.array(
[[0,0,0,3,0,0,0,0,0,0,0,0,0,0,0,0,3,0,0,0,3,0,2,0,0,1,0,0,0,0,0,0]
,[0,0,0,3,0,0,0,0,0,0,0,0,0,0,0,0,3,0,0,0,3,0,2,2,0,0,0,0,0,0,0,0]
,[0,0,0,3,0,0,0,0,2,2,2,0,0,0,0,0,3,0,0,0,3,0,0,2,2,2,2,2,2,2,2,2]
,[0,0,0,3,0,0,0,2,0,0,0,2,0,0,0,0,3,0,0,0,3,3,0,0,0,0,0,0,0,0,0,0]
,[0,0,0,3,0,0,2,0,1,0,0,0,2,0,0,0,3,0,0,0,0,3,3,3,3,3,0,0,0,0,0,0]
,[0,0,0,3,0,0,2,0,0,0,0,0,2,0,0,0,3,0,0,0,0,0,0,0,0,3,3,3,3,3,3,3]
,[0,0,0,3,0,0,2,0,0,0,0,0,2,0,0,0,3,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]
,[0,0,0,0,3,0,0,2,0,0,0,2,0,0,0,3,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]
,[0,0,0,0,3,0,0,0,2,2,2,0,0,0,0,3,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]
,[0,0,0,0,0,3,0,0,0,0,0,0,0,0,3,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]
,[0,0,0,0,0,0,3,0,0,0,0,0,0,3,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]
,[3,3,3,3,0,0,0,3,0,0,0,0,3,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]
,[0,0,0,3,0,0,0,0,3,3,3,3,0,0,0,0,0,3,3,3,3,0,0,0,0,0,0,0,0,0,0,0]
,[0,0,0,0,3,0,0,0,0,0,0,0,0,0,0,3,3,3,0,0,3,3,3,3,0,0,0,0,0,0,0,0]
,[0,0,0,0,3,3,0,0,0,0,0,0,0,0,0,3,0,0,0,0,0,0,0,3,0,0,0,0,0,0,0,0]
,[0,0,0,0,0,3,0,0,0,0,0,0,0,0,0,3,0,0,2,2,2,0,0,3,0,0,0,0,0,0,0,0]
,[2,2,2,0,0,3,0,0,0,0,0,0,0,0,0,3,0,0,2,1,2,0,0,3,0,0,0,0,0,0,0,0]
,[0,0,2,2,0,3,3,0,0,0,0,0,0,0,0,3,3,0,2,2,2,0,0,3,0,0,0,0,0,0,0,0]
,[0,0,0,2,0,0,3,0,0,0,0,0,0,0,0,0,3,0,0,0,0,0,0,3,0,0,0,0,0,0,0,0]
,[1,0,0,2,0,0,3,0,0,0,0,0,0,0,0,0,3,3,0,0,0,0,3,0,0,0,0,0,0,0,0,0]
,[0,0,0,2,0,0,3,0,0,0,0,0,0,0,0,0,0,3,3,0,3,3,0,0,0,0,0,0,0,0,0,0]
,[0,0,0,2,0,0,3,0,0,0,0,0,0,0,0,0,0,0,0,3,3,0,0,0,0,0,0,0,0,0,0,0]
,[0,0,2,2,0,0,3,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]
,[2,2,2,0,0,0,3,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]
,[0,0,0,0,0,3,3,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,3,3,3,3,3,3,3,3]
,[0,0,0,0,0,3,0,0,0,0,0,0,3,3,3,3,3,3,3,3,0,0,0,0,3,0,0,0,0,0,0,0]
,[0,0,0,3,3,0,0,0,0,3,3,3,3,2,2,2,2,2,2,3,3,0,0,0,3,0,0,0,0,0,2,2]
,[3,3,3,3,0,0,0,0,0,3,2,2,2,0,0,0,0,0,2,2,3,0,0,0,3,0,0,0,2,2,2,0]
,[0,0,0,0,0,0,0,0,0,3,2,0,0,0,0,0,0,0,0,2,3,0,0,0,3,0,0,2,2,0,0,0]
,[0,0,0,0,0,0,0,0,0,3,2,0,0,0,1,0,0,0,0,2,3,0,0,0,3,0,0,2,0,0,0,1]]
)

Which can be presented visually in a picture like this:

Where the red dots are numbered from left to right and can be identified in the matrix using the following function. Thanks to @DanielF in this answer

def getRedDotsCoordinatesFromLeftToRight(np_matrix, red_dor_number=1):
    red_dots = np.where(np_matrix == red_dor_number)
    red_dots = tuple(g[np.argsort(red_dots[-1])] for g in red_dots)
    red_dots = np.stack(red_dots)[::-1].T
    return red_dots

red_dots = getRedDotsCoordinatesFromLeftToRight(np_matrix)
print(red_dots)

red_dots = np.array(
    [[ 0, 25],
    [ 4,  8],
    [16, 19],
    [19,  0],
    [29, 14],
    [29, 31]]
)

Two questions:

Question 1: How can we identify all the white points coordinates (marked with 0) within the green boundaries (marked with 2) which are located with red dots (marked with 1) ?
Question 2: How can we identify all the white points coordinates (marked with 0) between black boundaries (marked with 3) and the green boundaries (marked with 2) which are located with red dots (marked with 1) ?

I am looking for this result for this example matrix:

space_within_greenDots = np.array(
    [[[17,  0], [17,  1], [18,  0], [18,  1], [18,  2], [19,  1], [19,  2], [20,  0], [20,  1], [20,  2], [21,  0], [21,  1], [21,  2], [22,  0], [22,  1]],
    [[ 3,  8], [ 3,  9], [ 3, 10], [ 4,  7], [ 4,  9], [ 4, 10], [ 4, 11], [ 5,  7], [ 5,  8], [ 5,  9], [ 5, 10], [ 5, 11], [ 6,  7], [ 6,  8], [ 6,  9], [ 6, 10], [ 6, 11], [ 7,  8], [ 7,  9], [ 7, 10]],
    [[27, 13], [27, 14], [27, 15], [27, 16], [27, 17], [28, 11], [28, 12], [28, 13], [28, 14], [28, 15], [28, 16], [28, 17], [28, 18], [29, 11], [29, 12], [29, 13], [29, 15], [29, 16], [29, 17], [29, 18]],
    [],
    [[ 0, 23], [ 0, 24], [ 0, 26], [ 0, 27], [ 0, 28], [ 0, 29], [ 0, 30], [ 0, 31], [ 1, 24], [ 1, 25], [ 1, 26], [ 1, 27], [ 1, 28], [ 1, 29], [ 1, 30], [ 1, 31]],
    [[27, 31], [28, 29], [28, 30], [28, 31], [29, 28], [29, 29], [29, 30]]],
)    


space_between_darkDots_and_greenDots = np.array(
    [ [[12,  0], [12,  1], [12,  2], [13,  0], [13,  1], [13,  2], [13,  3], [14,  0], [14,  1], [14,  2], [14,  3], [15,  0], [15,  1], [15,  2], [15,  3], [15,  4], [16,  3], [16,  4], [17,  4], [18,  4], [18,  5], [19,  4], [19,  5], [20,  4], [20,  5], [21,  4], [21,  5], [22,  4], [22,  5], [23,  3], [23,  4], [23,  5], [24,  0], [24,  1], [24,  2], [24,  3], [24,  4], [25,  0], [25,  1], [25,  2], [25,  3], [25,  4], [26,  0], [26,  1], [26,  2]],
    [[ 0,  4], [ 0,  5], [ 0,  6], [ 0,  7], [ 0,  8], [ 0,  9], [ 0, 10], [ 0, 11], [ 0, 12], [ 0, 13], [ 0, 14], [ 0, 15], [ 1,  4], [ 1,  5], [ 1,  6], [ 1,  7], [ 1,  8], [ 1,  9], [ 1, 10], [ 1, 11], [ 1, 12], [ 1, 13], [ 1, 14], [ 1, 15], [ 2,  4], [ 2,  5], [ 2,  6], [ 2,  7], [ 2, 11], [ 2, 12], [ 2, 13], [ 2, 14], [ 2, 15], [ 3,  4], [ 3,  5], [ 3,  6], [ 3, 12], [ 3, 13], [ 3, 14], [ 3, 15], [ 4,  4], [ 4,  5], [ 4, 13], [ 4, 14], [ 4, 15], [ 5,  4], [ 5,  5], [ 5, 13], [ 5, 14], [ 5, 15], [ 6,  4], [ 6,  5], [ 6, 13], [ 6, 14], [ 6, 15], [ 7,  5], [ 7,  6], [ 7, 12], [ 7, 13], [ 7, 14], [ 8,  5], [ 8,  6], [ 8,  7], [ 8, 11], [ 8, 12], [ 8, 13], [ 8, 14], [ 9,  6], [ 9,  7], [ 9,  8], [ 9,  9], [ 9, 10], [ 9, 11], [ 9, 12], [ 9, 13], [10,  7], [10,  8], [10,  9], [10, 10], [10, 11], [10, 12], [11,  8], [11,  9], [11, 10], [11, 11]],
    [],
    [[13, 18], [13, 19], [14, 16], [14, 17], [14, 18], [14, 19], [14, 20], [14, 21], [14, 22], [15, 16], [15, 17], [15, 21], [15, 22], [16, 16], [16, 17], [16, 21], [16, 22], [17, 17], [17, 21], [17, 22], [18, 17], [18, 18], [18, 19], [18, 20], [18, 21], [18, 22], [19, 18], [19, 19], [19, 20], [19, 21], [20, 19]],
    [[ 0, 21], [ 1, 21], [ 2, 21], [ 2, 22], [ 3, 22], [ 3, 23], [ 3, 24], [ 3, 25], [ 3, 26], [ 3, 27], [ 3, 28], [ 3, 29], [ 3, 30], [ 3, 31], [ 4, 26], [ 4, 27], [ 4, 28], [ 4, 29], [ 4, 30], [ 4, 31]],
    [[25, 25], [25, 26], [25, 27], [25, 28], [25, 29], [25, 30], [25, 31], [26, 25], [26, 26], [26, 27], [26, 28], [26, 29], [27, 25], [27, 26], [27, 27], [28, 25], [28, 26], [29, 25], [29, 26]],
    ]
)

A few assumptions:

The matrix shape can vary. It is not a fixed size.
The number of red dots varies from matrix to matrix. But there is always at least one red dot in the matrix.¨

https://www.learnopencv.com/blob-detection-using-opencv-python-c/ ?? - but I'm finding it difficult to install a opencv version — f5r5e5d, Nov 17 '17 at 21:29

Joe Iddon · Accepted Answer · 2019-09-24T19:21:34.253

Question 1 Solution using a recursive floodfill algorithm:

See the floodfill algorithm in this JavaScript demonstration I made. GitHub Source.

I created a floodfill function first that works just like a paint program i.e. when given a point in an enclosed region, will fill in that region up to the border with a colour.

Then, all that needed to be done was to go through each red pixel (value 1) and floodfill up to green pixels (value 2) with the colour of what index red dot we are on (so that we can get the regions separately later).

Then, we simply use a version of your red_dots program that I modified to be a bit more generalised to get the result of all the coordinates of the white pixels.

This last step is done in a one-liner. It converts everything to a big list where each sub-list contains coordinates of a region of white pixels.

Note how we must end with a list at the end as this is not a rectangular shape so cannot use a numpy array (unless we use dtype=object).

Anyway, here is the code:

import numpy as np

def inArrBounds(arr, c):
    return 0 <= c[0] < arr.shape[1] and 0 <= c[1] < arr.shape[0]

def floodfill(arr, start, fillCol, edgeCol):
    if arr[start[1],start[0]] in (fillCol, edgeCol):
        return
    arr[start[1], start[0]] = fillCol
    for p in ((start[0]+1, start[1]),
              (start[0]-1, start[1]), 
              (start[0], start[1]+1),
              (start[0], start[1]-1)):
        if inArrBounds(arr, p):
            floodfill(arr, p, fillCol, edgeCol)

def coordsLtR(arr, val):
    pnts = np.where(arr == val)
    pnts = tuple(g[np.argsort(pnts[-1])] for g in pnts)
    pnts = np.stack(pnts)[::-1].T
    return pnts

red_dots = coordsLtR(np_matrix, 1)
for i, dot in enumerate(red_dots):
    floodfill(np_matrix, dot, i+4, 2)
    np_matrix[dot[1], dot[0]] = 1

regions = [coordsLtR(np_matrix,i+4)[:,::-1].tolist() for i in range(len(red_dots))]

which creates the regions list as:

[[17, 0], [18, 0], [20, 0], [21, 0], [22, 0], [17, 1], [18, 1], [19, 1], [20, 1], [21, 1], [22, 1], [18, 2], [19, 2], [20, 2], [21, 2]]
[[4, 7], [6, 7], [5, 7], [3, 8], [7, 8], [6, 8], [5, 8], [6, 9], [7, 9], [5, 9], [4, 9], [3, 9], [5, 10], [4, 10], [3, 10], [6, 10], [7, 10], [5, 11], [6, 11], [4, 11]]
[[28, 11], [29, 11], [29, 12], [28, 12], [27, 13], [29, 13], [28, 13], [27, 14], [28, 14], [29, 15], [28, 15], [27, 15], [27, 16], [29, 16], [28, 16], [28, 17], [29, 17], [27, 17], [28, 18], [29, 18]]
[]
[[0, 23], [0, 24], [1, 24], [1, 25], [0, 26], [1, 26], [0, 27], [1, 27], [0, 28], [1, 28], [0, 29], [1, 29], [0, 30], [1, 30], [0, 31], [1, 31]]
[[29, 28], [28, 29], [29, 29], [28, 30], [29, 30], [27, 31], [28, 31]]

And to just visualise what the filled regions in np_matrix looks like, here is a screenshot from a matplotlib plot:

Question 2 Solution

The logic remains the same for this second section, just we have to do things in the right order. The way I would go about doing this would be to floodfill to the black borders with one colour and then subtract the white regions and green borders from this.

So, we need to work with a separate np_matrix as to not interfere with the first one. A copy can be made using np.copy.

We then need to fill in to the black border from the red dots and then from this filled in region, subtract all the coordinates that are in the white region or are green.

So, using the same functions from above, here is the code:

def validBlackCoord(c):
    return not (any(c in s for s in white_regions) or np_matrix[c[0],c[1]] == 2)

red_dots = coordsLtR(np_matrix, 1)
white_matrix = np.copy(np_matrix)
for i, dot in enumerate(red_dots):
    floodfill(white_matrix, dot, i+4, 2)
    white_matrix[dot[1], dot[0]] = 1

white_regions = [coordsLtR(white_matrix,i+4)[:,::-1].tolist() for i in range(len(red_dots))]

black_matrix = np.copy(np_matrix)
for i, dot in enumerate(red_dots):
    floodfill(black_matrix, dot, i+4, 3)
    black_matrix[dot[1], dot[0]] = 1

black_regions = [coordsLtR(black_matrix,i+4)[:,::-1].tolist() for i in range(len(red_dots))]

black_regions = [list(filter(key=validBlackCoord, r)) for r in black_regions]

which creates both lists, white_regions is the same as above and black_regions is:

[[12, 0], [24, 0], [15, 0], [25, 0], [14, 0], [13, 0], [26, 0], [24, 1], [15, 1], [14, 1], [25, 1], [13, 1], [12, 1], [26, 1], [24, 2], [25, 2], [26, 2], [12, 2], [15, 2], [13, 2], [14, 2], [24, 3], [14, 3], [15, 3], [23, 3], [16, 3], [13, 3], [25, 3], [22, 4], [19, 4], [21, 4], [15, 4], [17, 4], [23, 4], [25, 4], [20, 4], [18, 4], [24, 4], [16, 4], [22, 5], [21, 5], [20, 5], [18, 5], [23, 5], [19, 5]]
[[0, 4], [6, 4], [5, 4], [4, 4], [3, 4], [2, 4], [1, 4], [8, 5], [7, 5], [6, 5], [4, 5], [3, 5], [2, 5], [5, 5], [1, 5], [0, 5], [1, 6], [3, 6], [9, 6], [0, 6], [7, 6], [8, 6], [2, 6], [8, 7], [9, 7], [2, 7], [10, 7], [0, 7], [1, 7], [0, 8], [1, 8], [9, 8], [11, 8], [10, 8], [0, 9], [1, 9], [11, 9], [10, 9], [9, 9], [1, 10], [10, 10], [0, 10], [9, 10], [11, 10], [10, 11], [9, 11], [8, 11], [11, 11], [1, 11], [2, 11], [0, 11], [0, 12], [1, 12], [10, 12], [9, 12], [2, 12], [8, 12], [3, 12], [7, 12], [2, 13], [6, 13], [3, 13], [4, 13], [1, 13], [8, 13], [0, 13], [9, 13], [7, 13], [5, 13], [6, 14], [1, 14], [0, 14], [7, 14], [2, 14], [8, 14], [4, 14], [3, 14], [5, 14], [6, 15], [2, 15], [0, 15], [1, 15], [5, 15], [3, 15], [4, 15]]
[]
[[14, 16], [15, 16], [16, 16], [18, 17], [17, 17], [15, 17], [16, 17], [14, 17], [18, 18], [19, 18], [14, 18], [13, 18], [19, 19], [18, 19], [20, 19], [13, 19], [14, 19], [19, 20], [18, 20], [14, 20], [18, 21], [19, 21], [17, 21], [15, 21], [16, 21], [14, 21], [15, 22], [17, 22], [18, 22], [16, 22], [14, 22]]
[[0, 21], [2, 21], [1, 21], [3, 22], [2, 22], [3, 23], [3, 24], [3, 25], [3, 26], [4, 26], [4, 27], [3, 27], [4, 28], [3, 28], [3, 29], [4, 29], [3, 30], [4, 30], [3, 31], [4, 31]]
[[25, 25], [29, 25], [26, 25], [28, 25], [27, 25], [25, 26], [29, 26], [28, 26], [26, 26], [27, 26], [27, 27], [25, 27], [26, 27], [26, 28], [25, 28], [26, 29], [25, 29], [25, 30], [25, 31]]

this is great @JoeIddon, thank you. I will try to see if i can use your solution to solve the second question also — RaduS, Nov 18 '17 at 07:18
Can't we use a green dot as a seed for finding the black area. Just like using the red dot as a seed for finding the green area? — RaduS, Nov 18 '17 at 07:39
The problem with that is we would floodfilll into the middle of the `green` region rather than just out to the `black` region... — Joe Iddon, Nov 18 '17 at 07:40
But once we have all the green dots we can just flood fill the black area and ignore the green dots and the red dot. Flood fill black area and excluding the known green dots and red dot inside it — RaduS, Nov 18 '17 at 07:43
By excluding the known green dots and red dot, not only do we find the black area but we can also add extra layers on top of the black area and find those in exactly the same manner — RaduS, Nov 18 '17 at 07:53
That's what I am writing kinda, nearly done, just editing the answer — Joe Iddon, Nov 18 '17 at 07:58
@RaduS I added a link to a JS demonstration of the algorithm if you wanted to take a look at that for no reason, just out of interest in the recursion. — Joe Iddon, Nov 18 '17 at 16:09
I notice a strange error on a bigger matrix and area to fill. My test matrix has a shape of a 2000x2000 and the area to fill is about 500x500. Then I get this error : `Fatal Python error: Cannot recover from stack overflow.` — RaduS, Nov 19 '17 at 10:30

B. M. · Answer 2 · 2017-11-20T18:30:06.930

An other iterative paint algorithm implementation, with arrays for vectored exploration, and sets for selection.

around =array([[[ 0,  1]],[[-1,  0]],[[ 1,  0]],[[ 0, -1]]])

def grow(seed,color):
    filled=set()
    current = set(tuple(x) for x in seed)
    while current :
        seed=np.vstack(current)
        x,y = (around+seed).reshape(-1,2).T
        np.clip(x,0,m.shape[0]-1,x)
        np.clip(y,0,m.shape[1]-1,y)
        good = (m[x,y]==color)
        win = np.vstack((x[good],y[good])).T
        front=set(tuple(x) for x in win)           
        current = front - filled
        filled |= current
    return np.vstack(filled) if filled else None

mout=m
seed=(vstack(np.where(m==1)).T)[:,None]
areas=dict()
n=4    

for color in (0,2,0,3):
     next=[ grow(s,color) for s in seed]
     areas[n]=next
     st=np.vstack(s for s in next if not s is None)  
     x,y=st.T
     mout[x,y] = n
     n +=1
     seed = [ x if x is not None else y for (x,y) in zip(next,seed) ]

imshow(mout)

For :

Edit

A pure set solution, simpler and faster on this example:

def grows(current,color,m):
    ra,rb=m.shape 
    filled=set()
    while current :
        next0={(a-1,b) for (a,b) in current if a>0}\
        | {(a,b-1) for (a,b) in current if b>0}\
        | {(a+1,b) for (a,b) in current if a<ra-1}\
        | {(a,b+1) for (a,b) in current if b<rb-1}        
        next = { p for p in next0 if m[p]==color}           
        current = next - filled
        filled |= current
    return filled

seed2=[set([p]) for p in zip(*np.where(m==1))]

def m2(seed,m):
    mout=m.copy()
    areas=dict()
    for i,color in enumerate((0,2,0,3)):
        next = [grows(s,color,mout) for s in seed]
        areas[i]=next
        for s in next :
            for p in s: 
                mout[p] = 4+i
        seed=[x or y for x,y in zip(next,seed)]
    return mout,areas 

mout,areas = m2(seed2,m)
imshow(mout)

This is awesome. It works on really big arrays. But how do we get the two outputs, one for all the green points and one for all the black points? Just like in the question? The only output I have now is the picture but this doesn't help much — RaduS, Nov 19 '17 at 23:17
all is in the areas dict : areas[4] is the first zone and so on. I add a pure set solution, 3x faster on this example. — B. M., Nov 20 '17 at 17:54
What is `ra` and `rb`? They are unresolved variables in the edit. — RaduS, Nov 20 '17 at 18:10

Get all coordinates points within known boundaries in a numpy matrix for each dot

2 Answers2