How can I plot a heatmap on a sphere given a list of latitudes and longitudes?

Question

I have a list of over 500 points, given in Latitude and Longitudes. These points represent craters, and I want to plot a heatmap of these craters. For example, I want an area with a lot of craters to be considered "hot" and fewer craters to be "cold". I have looked at KDE using SciPy, and also tried using ListSliceDensityPlot3D in Mathematica, but I have been unable to create a graph that is adequate.

I converted each point from latitude/longitude into Cartesian [x,y,z] coordinates, and plotted them on the surface of a sphere, but I don't know how I would take the list of points and calculate the density in a given area, and then plot it on a 3D surface.

The idea being that I obtain a plot something like this image of Ceres!

Thanks in advance, please ask questions if needed, sorry if I didn't post enough information initially.

Answer 1

This is sort of a brute force method, but it works up to a certain point. It will be problematic, if you make the mesh extremely fine or have thousands of craters. If the bin size is small enough there is no big difference between the distance on the surface and the 3D distance, so I took the latter, as it is easier to calculate, but one may want to change this.

Code looks like:

from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import cm


def random_point( r=1 ):
    ct = 2*np.random.rand() - 1
    st = np.sqrt( 1 - ct**2 )
    phi = 2* np.pi *  np.random.rand()
    x = r * st * np.cos( phi)
    y = r * st * np.sin( phi)
    z = r * ct
    return np.array( [x, y, z ] )

def near( p, pntList, d0 ):
    cnt=0
    for pj in pntList:
        dist=np.linalg.norm( p - pj )
        if dist < d0:
            cnt += 1 - dist/d0
    return cnt


"""
https://stackoverflow.com/questions/22128909/plotting-the-temperature-distribution-on-a-sphere-with-python
"""

pointList = np.array([ random_point( 10.05 ) for i in range( 65 ) ] )

fig = plt.figure()
ax = fig.add_subplot( 1, 1, 1, projection='3d')

u = np.linspace( 0, 2 * np.pi, 120)
v = np.linspace( 0, np.pi, 60 )

# create the sphere surface
XX = 10 * np.outer( np.cos( u ), np.sin( v ) )
YY = 10 * np.outer( np.sin( u ), np.sin( v ) )
ZZ = 10 * np.outer( np.ones( np.size( u ) ), np.cos( v ) )

WW = XX.copy()
for i in range( len( XX ) ):
    for j in range( len( XX[0] ) ):
        x = XX[ i, j ]
        y = YY[ i, j ]
        z = ZZ[ i, j ]
        WW[ i, j ] = near(n p.array( [x, y, z ] ), pointList, 3)
WW = WW / np.amax( WW )
myheatmap = WW

# ~ ax.scatter( *zip( *pointList ), color='#dd00dd' )
ax.plot_surface( XX, YY,  ZZ, cstride=1, rstride=1, facecolors=cm.jet( myheatmap ) )
plt.show() 

Outcome is like:

You can also modify the distance function to account for crater size, maybe.

Answer 2

There's two separate problems here: defining suitable bin sizes and count functions on a sphere so that you can build an appropriate colour function, and then plotting that colour function on a 3D sphere. I'll provide a Mathematica solution for both.

1. Making up example data

To start with, here's some example data:

data = Map[
  Apply@Function[{x, y, z},
    {
     Mod[ArcTan[x, y], 2 π],
     ArcSin[z/Sqrt[x^2 + y^2 + z^2]]
     }
    ],
  Map[
   #/Norm[#]&,
   Select[
    RandomReal[{-1, 1}, {200000, 3}],
    And[
      Norm[#] > 0.01,
      Or[
       Norm[# - {0, 0.3, 0.2}] < 0.6,
       Norm[# - {-0.3, -0.15, -0.3}] < 0.3
       ]
      ] &
    ]
   ]
  ]

I've made it a bit lumpy so that it will have more interesting features when it comes to plot time.

2. Building a colour function

To build a colour function within Mathematica, the cleanest solution is to use HistogramList, but this needs to be modified to account for the fact that bins at high latitude will have different areas, so the density needs to be adjusted.

Nevertheless, the in-built histogram-building tools are pretty good:

DensityHistogram[
 data,
 {5°}
 , AspectRatio -> Automatic
 , PlotRangePadding -> None
 , ImageSize -> 700
 ]

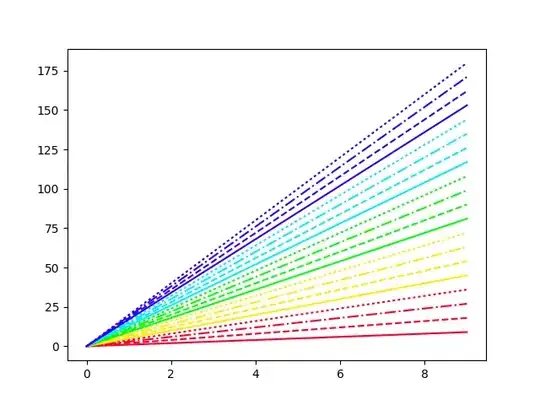
You can get the raw data via

{{ϕbins, θbins}, counts} =  HistogramList[data, {15°}]

and then for convenience let's define

ϕcenters = 1/2 (Most[ϕbins] + Rest[ϕbins])
θcenters = 1/2 (Most[θbins] + Rest[θbins])

with the bin area calculated using

SectorArea[ϕmin_, ϕmax_, θmin_, θmax_] = (Abs[ϕmax - ϕmin]/(4 π)) * 
                                         Integrate[Sin[θ], {θ, θmin, θmax}]

This then allows you to define your own color function as

function[ϕ_, θ_] := With[{
   iϕ = First[Nearest[ϕcenters -> Range[Length[ϕcenters]], ϕ]],
   iθ = First[Nearest[θcenters -> Range[Length[θcenters]], θ]]
   },
  (N@counts[[iϕ, iθ]]/
   SectorArea[ϕbins[[iϕ]], ϕbins[[iϕ + 1]], θbins[[iθ]], θbins[[iθ + 1]]])/max
  ]

So, here's that function in action:

texture = ListDensityPlot[
  Flatten[
   Table[
    {
     ϕcenters[[iϕ]],
     θcenters[[iθ]],
     function[ϕcenters[[iϕ]], θcenters[[iθ]]]
     }
    , {iϕ, Length[ϕbins] - 1}
    , {iθ, Length[θbins] - 1}
    ], 1]
  , InterpolationOrder -> 0
  , AspectRatio -> Automatic
  , ColorFunction -> ColorData["GreenBrownTerrain"]
  , Frame -> None
  , PlotRangePadding -> None
  ]

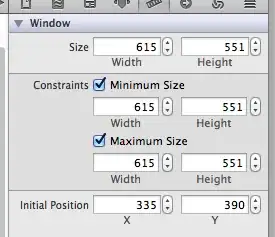
3. Plotting

To plot the data on a sphere, I see two main options: you can make a surface plot and then wrap that around a parametric plot as a Texture, as in

ParametricPlot3D[
 {Cos[ϕ] Sin[θ], Sin[ϕ] Sin[θ], 
  Cos[θ]}
 , {ϕ, 0, 2 π}, {θ, 0, π}
 , Mesh -> None
 , Lighting -> "Neutral"
 , PlotStyle -> Directive[
   Specularity[White, 30],
   Texture[texture]
   ]
 ]

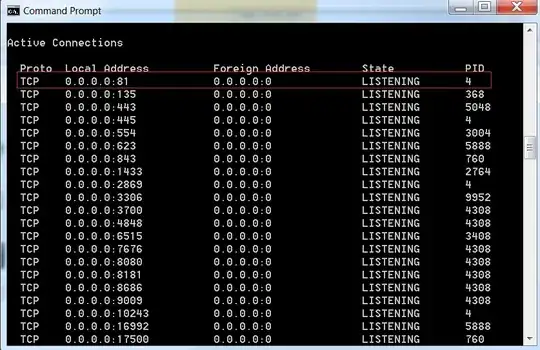
Or you can define it as an explicit ColorFunction in that same parametric plot:

ParametricPlot3D[
 {Cos[ϕ] Sin[θ], Sin[ϕ] Sin[θ], 
  Cos[θ]}
 , {ϕ, 0, 2 π}, {θ, 0, π}
 , ColorFunctionScaling -> False
 , ColorFunction -> Function[{x, y, z, ϕ, θ},
   ColorData["GreenBrownTerrain"][function[ϕ, θ]]
   ]
 ]

---

All of the above is of course very modular, so you're free to mix-and-match to your advantage.