0

How do you implement the rotation of the shape in place and the movement in a rotated state? I want to move the rotated shape towards the x and y axes of the screen I see.

I have already made the shape move in the direction of the x-axis and y-axis when I press the key. But I can't move the way I want to. It's weird. How do I set up the code to move the way I want to? I'll put the code up for now.

glTranslatef(2.5 + puzX1, 2 + puzY1, 0);
glRotatef(100, 0.0, 0.0, 1.0);
glRotatef(puzang1, 0.0, 0.0, 1.0);
glTranslatef(-2.5+puzX1, -2+puzY1, 0);

I wrote the code to make it spin in place.

The code at the top and bottom of the code is a code that moves to the center of the shape and then returns it to its place.

What should I add? Which part should be modified?

I am not good at English. i'm so sorry Can you help me?

Rabbid76
  • 202,892
  • 27
  • 131
  • 174
정나영
  • 65
  • 7

1 Answers1

2

Note, that drawing by glBegin/glEnd sequences, the fixed function pipeline matrix stack, is deprecated since decades. Read about Fixed Function Pipeline and see Vertex Specification and Shader for a state of the art way of rendering.

How do you implement the rotation of the shape in place?

If the shade should rotate on its local axis, then you have to do the rotation before the translation. In the code this means the rotation instruction has to be after the translation instruction:

glTranslatef(2.5 + puzX1, 2 + puzY1, 0);
glRotatef(puzang1, 0.0, 0.0, 1.0);
glRotatef(100, 0.0, 0.0, 1.0);

See also OpenGL translation before and after a rotation


Explanation:

Translation: See the documentation of glTranslate:

glTranslate produces a translation by x y z . The current matrix (see glMatrixMode) is multiplied by this translation matrix, with the product replacing the current matrix.

Rotation: See the documentation of glRotate:

glRotate produces a rotation of angle degrees around the vector x y z . The current matrix (see glMatrixMode) is multiplied by a rotation matrix with the product replacing the current matrix.


The translation matrix looks like this:

Matrix4x4 translate;

translate[0] : ( 1,  0,  0,  0 )
translate[1] : ( 0,  1,  0,  0 )
translate[2] : ( 0,  0,  1,  0 )
translate[3] : ( tx, ty, tz, 1 )

And the rotation matrix around Z-Axis looks like this:

Matrix4x4  rotate;
float      angle;

rotate[0] : ( cos(angle),  sin(angle), 0, 0 )
rotate[1] : ( -sin(angle), cos(angle), 0, 0 )
rotate[2] : ( 0,           0,          1, 0 )
rotate[3] : ( 0,           0,          0, 1 )


The result of translate * rotate is this:

glTranslate( ..... );
glRotate( ..... );


model[0] : ( cos(angle),  sin(angle), 0,  0 )
model[1] : ( -sin(angle), cos(angle), 0,  0 )
model[2] : ( 0,           1,          0,  0 )
model[3] : ( tx,          ty,         tz, 1 )


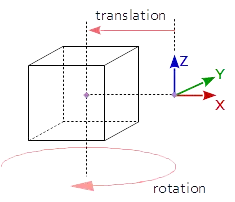
The result of rotate * translate is:

glRotate( ..... );
glTranslate( ..... );


model[0] : ( cos(angle),                     sin(angle),                     0,  0 )
model[1] : ( -sin(angle),                    cos(angle),                     0,  0 )
model[2] : ( 0,                              0,                              1,  0 )
model[3] : ( cos(angle)*tx - sin(angle)*tx,  sin(angle)*ty + cos(angle)*ty,  tz, 1 )

Rabbid76
  • 202,892
  • 27
  • 131
  • 174