Getting the circumcentres from a delaunay triangulation generated using matplotlib

Question

If I use matplotlib to generate a delaunay triangulation for a group of points, what is the most appropraite way of getting the circumcentres of the triangles that have been geenrated? I haven't yet managed to find an obvious method in the Triangulation library to do this.

Answer 1

You should be able to calculate it using matplotlib.delaunay.triangulate.Triangulation:

Triangulation(x, y) x, y -- the coordinates of the points as 1-D arrays of floats

. . .

Attributes: (all should be treated as read-only to maintain consistency) x, y -- the coordinates of the points as 1-D arrays of floats.

  circumcenters -- (ntriangles, 2) array of floats giving the (x,y)
    coordinates of the circumcenters of each triangle (indexed by a triangle_id).

Adapted from one of the matplotlib examples (there is probably a cleaner way to do this, but it should work):

import matplotlib.pyplot as plt
import matplotlib.delaunay
import matplotlib.tri as tri
import numpy as np
import math

# Creating a Triangulation without specifying the triangles results in the
# Delaunay triangulation of the points.

# First create the x and y coordinates of the points.
n_angles = 36
n_radii = 8
min_radius = 0.25
radii = np.linspace(min_radius, 0.95, n_radii)

angles = np.linspace(0, 2*math.pi, n_angles, endpoint=False)
angles = np.repeat(angles[...,np.newaxis], n_radii, axis=1)
angles[:,1::2] += math.pi/n_angles

x = (radii*np.cos(angles)).flatten()
y = (radii*np.sin(angles)).flatten()

tt = matplotlib.delaunay.triangulate.Triangulation(x,y)
triang = tri.Triangulation(x, y)

# Plot the triangulation.
plt.figure()
plt.gca().set_aspect('equal')
plt.triplot(triang, 'bo-')

plt.plot(tt.circumcenters[:,0],tt.circumcenters[:,1],'r.')
plt.show()

Answer 2

Here is a function that computes them. It can also be used on other triangulation structures, e.g. scipy's Delaunay triangulation (see below).

def compute_triangle_circumcenters(xy_pts, tri_arr):
    """
    Compute the centers of the circumscribing circle of each triangle in a triangulation.
    :param np.array xy_pts : points array of shape (n, 2)
    :param np.array tri_arr : triangles array of shape (m, 3), each row is a triple of indices in the xy_pts array

    :return: circumcenter points array of shape (m, 2)
    """
    tri_pts = xy_pts[tri_arr]  # (m, 3, 2) - triangles as points (not indices)

    # finding the circumcenter (x, y) of a triangle defined by three points:
    # (x-x0)**2 + (y-y0)**2 = (x-x1)**2 + (y-y1)**2
    # (x-x0)**2 + (y-y0)**2 = (x-x2)**2 + (y-y2)**2
    #
    # becomes two linear equations (squares are canceled):
    # 2(x1-x0)*x + 2(y1-y0)*y = (x1**2 + y1**2) - (x0**2 + y0**2)
    # 2(x2-x0)*x + 2(y2-y0)*y = (x2**2 + y2**2) - (x0**2 + y0**2)
    a = 2 * (tri_pts[:, 1, 0] - tri_pts[:, 0, 0])
    b = 2 * (tri_pts[:, 1, 1] - tri_pts[:, 0, 1])
    c = 2 * (tri_pts[:, 2, 0] - tri_pts[:, 0, 0])
    d = 2 * (tri_pts[:, 2, 1] - tri_pts[:, 0, 1])

    v1 = (tri_pts[:, 1, 0] ** 2 + tri_pts[:, 1, 1] ** 2) - (tri_pts[:, 0, 0] ** 2 + tri_pts[:, 0, 1] ** 2)
    v2 = (tri_pts[:, 2, 0] ** 2 + tri_pts[:, 2, 1] ** 2) - (tri_pts[:, 0, 0] ** 2 + tri_pts[:, 0, 1] ** 2)

    # solve 2x2 system (see https://en.wikipedia.org/wiki/Invertible_matrix#Inversion_of_2_%C3%97_2_matrices)
    det = (a * d - b * c)
    detx = (v1 * d - v2 * b)
    dety = (a * v2 - c * v1)

    x = detx / det
    y = dety / det

    return (np.vstack((x, y))).T

On the data from @JoshAdel's answer above, adding the following code:

cc = compute_triangle_circumcenters(np.vstack([tt.x, tt.y]).T, tt.triangle_nodes)
plt.plot(cc[:, 0], cc[:, 1], ".k")

I get the following figure:

It can also be used on scipy.spatial.Delaunay like this:

from scipy.spatial import Delaunay
xy_pts = np.vstack([x, y]).T
dt = Delaunay(xy_pts)
cc = compute_triangle_circumcenters(dt.points, dt.simplices)

Answer 3

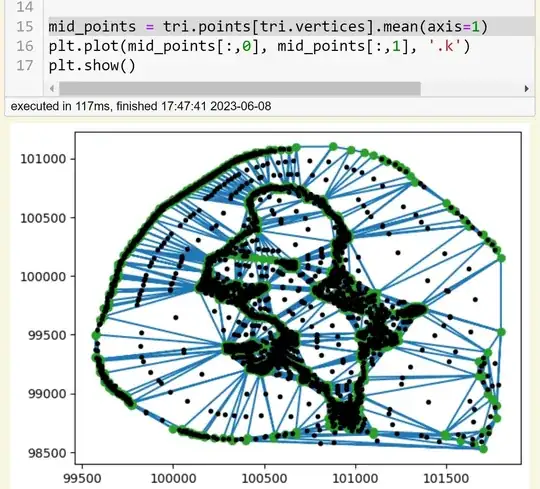
I think that solution is too overkill.. you can directly mean out the vertices of each triangle, like:

mid_points = tri.points[tri.vertices].mean(axis=1)