Vectorizing a "pure" function with numpy, assuming many duplicates

Question

I want to apply a "black box" Python function f to a large array arr. Additional assumptions are:

• Function f is "pure", e.g. is deterministic with no side effects.
• Array arr has a small number of unique elements.

I can achieve this with a decorator that computes f for each unique element of arr as follows:

import numpy as np
from time import sleep
from functools import wraps


N = 1000
np.random.seed(0)
arr = np.random.randint(0, 10, size=(N, 2))


def vectorize_pure(f):
    @wraps(f)
    def f_vec(arr):
        uniques, ix = np.unique(arr, return_inverse=True)
        f_range = np.array([f(x) for x in uniques])
        return f_range[ix].reshape(arr.shape)
    return f_vec


@np.vectorize
def usual_vectorize(x):
    sleep(0.001)
    return x


@vectorize_pure
def pure_vectorize(x):
    sleep(0.001)
    return x

# In [47]: %timeit usual_vectorize(arr)                                
# 1.33 s ± 6.16 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
# In [48]: %timeit pure_vectorize(arr)                                 
# 13.6 ms ± 81.8 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)

My concern is that np.unique sorts arr under the hood, which seems inefficient given the assumptions. I am looking for a practical way of implementing a similar decorator that

1. Takes advantage of fast numpy vectorized operations.
2. Does not sort the input array.

---

I suspect that the answer is "yes" using numba, but I would be especially interested in a numpy solution.

Also, it seems that depending on the arr datatype, numpy may use radix sort, so performance of unique may be good in some cases.

---

I found a workaround below, using pandas.unique; however, it still requires two passes over the original array, and pandas.unique does some extra work. I wonder if a better solution exists with pandas._libs.hashtable and cython, or anything else.

Answer 1

You actually can do this in one-pass over the array, however it requires that you know the dtype of the result beforehand. Otherwise you need a second-pass over the elements to determine it.

Neglecting the performance (and the functools.wraps) for a moment an implementation could look like this:

def vectorize_cached(output_dtype):
    def vectorize_cached_factory(f):
        def f_vec(arr):
            flattened = arr.ravel()
            if output_dtype is None:
                result = np.empty_like(flattened)
            else:
                result = np.empty(arr.size, output_dtype)

            cache = {}
            for idx, item in enumerate(flattened):
                res = cache.get(item)
                if res is None:
                    res = f(item)
                    cache[item] = res
                result[idx] = res
            return result.reshape(arr.shape)
        return f_vec
    return vectorize_cached_factory

It first creates the result array, then it iterates over the input array. The function is called (and the result stored) once an element is encountered that's not already in the dictionary - otherwise it simply uses the value stored in the dictionary.

@vectorize_cached(np.float64)
def t(x):
    print(x)
    return x + 2.5

>>> t(np.array([1,1,1,2,2,2,3,3,1,1,1]))
1
2
3
array([3.5, 3.5, 3.5, 4.5, 4.5, 4.5, 5.5, 5.5, 3.5, 3.5, 3.5])

However this isn't particularly fast because we're doing a Python loop over a NumPy array.

A Cython solution

To make it faster we can actually port this implementation to Cython (currently only supporting float32, float64, int32, int64, uint32, and uint64 but almost trivial to extend because it uses fused-types):

%%cython

cimport numpy as cnp

ctypedef fused input_type:
    cnp.float32_t
    cnp.float64_t
    cnp.uint32_t
    cnp.uint64_t
    cnp.int32_t
    cnp.int64_t

ctypedef fused result_type:
    cnp.float32_t
    cnp.float64_t
    cnp.uint32_t
    cnp.uint64_t
    cnp.int32_t
    cnp.int64_t

cpdef void vectorized_cached_impl(input_type[:] array, result_type[:] result, object func):
    cdef dict cache = {}
    cdef Py_ssize_t idx
    cdef input_type item
    for idx in range(array.size):
        item = array[idx]
        res = cache.get(item)
        if res is None:
            res = func(item)
            cache[item] = res
        result[idx] = res

With a Python decorator (the following code is not compiled with Cython):

def vectorize_cached_cython(output_dtype):
    def vectorize_cached_factory(f):
        def f_vec(arr):
            flattened = arr.ravel()
            if output_dtype is None:
                result = np.empty_like(flattened)
            else:
                result = np.empty(arr.size, output_dtype)

            vectorized_cached_impl(flattened, result, f)

            return result.reshape(arr.shape)
        return f_vec
    return vectorize_cached_factory

Again this only does one-pass and only applies the function once per unique value:

@vectorize_cached_cython(np.float64)
def t(x):
    print(x)
    return x + 2.5

>>> t(np.array([1,1,1,2,2,2,3,3,1,1,1]))
1
2
3
array([3.5, 3.5, 3.5, 4.5, 4.5, 4.5, 5.5, 5.5, 3.5, 3.5, 3.5])

Benchmark: Fast function, lots of duplicates

But the question is: Does it make sense to use Cython here?

I did a quick benchmark (without sleep) to get an idea how different the performance is (using my library simple_benchmark):

def func_to_vectorize(x):
    return x

usual_vectorize = np.vectorize(func_to_vectorize)
pure_vectorize = vectorize_pure(func_to_vectorize)
pandas_vectorize = vectorize_with_pandas(func_to_vectorize)
cached_vectorize = vectorize_cached(None)(func_to_vectorize) 
cython_vectorize = vectorize_cached_cython(None)(func_to_vectorize) 


from simple_benchmark import BenchmarkBuilder

b = BenchmarkBuilder()
b.add_function(alias='usual_vectorize')(usual_vectorize)
b.add_function(alias='pure_vectorize')(pure_vectorize)
b.add_function(alias='pandas_vectorize')(pandas_vectorize)
b.add_function(alias='cached_vectorize')(cached_vectorize)
b.add_function(alias='cython_vectorize')(cython_vectorize)

@b.add_arguments('array size')
def argument_provider():
    np.random.seed(0)
    for exponent in range(6, 20):
        size = 2**exponent
        yield size, np.random.randint(0, 10, size=(size, 2))

r = b.run()
r.plot()

According to these times the ranking would be (fastest to slowest):

• Cython version
• Pandas solution (from another answer)
• Pure solution (original post)
• NumPys vectorize
• The non-Cython version using Cache

The plain NumPy solution is only a factor 5-10 slower if the function call is very inexpensive. The pandas solution also has a much bigger constant factor, making it the slowest for very small arrays.

Benchmark: expensive function (time.sleep(0.001)), lots of duplicates

In case the function call is actually expensive (like with time.sleep) the np.vectorize solution will be a lot slower, however there is much less difference between the other solutions:

# This shows only the difference compared to the previous benchmark
def func_to_vectorize(x):
    sleep(0.001)
    return x

@b.add_arguments('array size')
def argument_provider():
    np.random.seed(0)
    for exponent in range(5, 10):
        size = 2**exponent
        yield size, np.random.randint(0, 10, size=(size, 2))

Benchmark: Fast function, few duplicates

However if you don't have that many duplicates the plain np.vectorize is almost as fast as the pure and pandas solution and only a bit slower than the Cython version:

# Again just difference to the original benchmark is shown
@b.add_arguments('array size')
def argument_provider():
    np.random.seed(0)
    for exponent in range(6, 20):
        size = 2**exponent
        # Maximum value is now depending on the size to ensures there 
        # are less duplicates in the array
        yield size, np.random.randint(0, size // 10, size=(size, 2))

Answer 2

This problem is actually quite interesting as it is a perfect example of a trade off between computation time and memory consumption.

From an algorithmic perspective finding the unique elements, and eventually computing only unique elements, can be achieved in two ways:

• two-(or more) passes approach:

  • find out all unique elements
  • find out where the unique elements are
  • compute the function on the unique elements
  • put all computed unique elements into the right place

• single-pass approach:

  • compute elements on the go and cache results
  • if an element is in the cache get it from there

The algorithmic complexity depends on the size of the input N and on the number of unique elements U. The latter can be formalized also using the r = U / N ratio of unique elements.

The more-passes approaches are theoretically slower. However, they are quite competitive for small N and U. The single-pass approaches are theoretically faster, but this would also strongly depends on the caching approaches and how they do perform depending on U. Of course, no matter how important is the asymptotic behavior, the actual timings do depend on the constant computation time factors. The most relevant in this problem is the func() computation time.

Approaches

A number of approaches can be compared:

• not cached

  • pure() this would be the base function and could be already vectorized
  • np.vectorized() this would be the NumPy standard vectorization decorator

• more-passes approaches

  • np_unique(): the unique values are found using np.unique() and uses indexing (from np.unique() output) for constructing the result (essentially equivalent to vectorize_pure() from here)
  • pd_unique(): the unique values are found using pd.unique() and uses indexing (via np.searchsorted()) for constructing the result(essentially equivalent to vectorize_with_pandas() from here)
  • set_unique(): the unique values are found using simply set() and uses indexing (via np.searchsorted()) for constructing the result
  • set_unique_msk(): the unique values are found using simply set() (like set_unique()) and uses looping and masking for constructing the result (instead of indexing)
  • nb_unique(): the unique values and their indexes are found using explicit looping with numba JIT acceleration
  • cy_unique(): the unique values and their indexes are found using explicit looping with cython

• single-pass approaches

  • cached_dict(): uses a Python dict for the caching (O(1) look-up)
  • cached_dict_cy(): same as above but with Cython (essentially equivalent to vectorized_cached_impl() from here)
  • cached_arr_cy(): uses an array for the caching (O(U) look-up)

pure()

def pure(x):
    return 2 * x

np.vectorized()

import numpy as np


vectorized = np.vectorize(pure)
vectorized.__name__ = 'vectorized'

np_unique()

import functools
import numpy as np


def vectorize_np_unique(func):
    @functools.wraps(func)
    def func_vect(arr):
        uniques, ix = np.unique(arr, return_inverse=True)
        result = np.array([func(x) for x in uniques])
        return result[ix].reshape(arr.shape)
    return func_vect

np_unique = vectorize_np_unique(pure)
np_unique.__name__ = 'np_unique'

pd_unique()

import functools
import numpy as np
import pandas as pd


def vectorize_pd_unique(func):
    @functools.wraps(func)
    def func_vect(arr):
        shape = arr.shape
        arr = arr.ravel()
        uniques = np.sort(pd.unique(arr))
        f_range = np.array([func(x) for x in uniques])
        return f_range[np.searchsorted(uniques, arr)].reshape(shape)
    return func_vect

pd_unique = vectorize_pd_unique(pure)
pd_unique.__name__ = 'pd_unique'

set_unique()

import functools


def vectorize_set_unique(func):
    @functools.wraps(func)
    def func_vect(arr):
        shape = arr.shape
        arr = arr.ravel()
        uniques = sorted(set(arr))
        result = np.array([func(x) for x in uniques])
        return result[np.searchsorted(uniques, arr)].reshape(shape)
    return func_vect

set_unique = vectorize_set_unique(pure)
set_unique.__name__ = 'set_unique'

set_unique_msk()

import functools


def vectorize_set_unique_msk(func):
    @functools.wraps(func)
    def func_vect(arr):
        result = np.empty_like(arr)
        for x in set(arr.ravel()):
            result[arr == x] = func(x)
        return result
    return func_vect

set_unique_msk = vectorize_set_unique_msk(pure)
set_unique_msk.__name__ = 'set_unique_msk'

nb_unique()

import functools
import numpy as np
import numba as nb
import flyingcircus as fc


@nb.jit(forceobj=False, nopython=True, nogil=True, parallel=True)
def numba_unique(arr, max_uniques):
    ix = np.empty(arr.size, dtype=np.int64)
    uniques = np.empty(max_uniques, dtype=arr.dtype)
    j = 0
    for i in range(arr.size):
        found = False
        for k in nb.prange(j):
            if arr[i] == uniques[k]:
                found = True
                break
        if not found:
            uniques[j] = arr[i]
            j += 1            
    uniques = np.sort(uniques[:j])
    # : get indices
    num_uniques = j
    for j in nb.prange(num_uniques):
        x = uniques[j]
        for i in nb.prange(arr.size):
            if arr[i] == x:
                ix[i] = j
    return uniques, ix


@fc.base.parametric
def vectorize_nb_unique(func, max_uniques=-1):
    @functools.wraps(func)
    def func_vect(arr):
        nonlocal max_uniques
        shape = arr.shape
        arr = arr.ravel()
        if max_uniques <= 0:
            m = arr.size
        elif isinstance(max_uniques, int):
            m = min(max_uniques, arr.size)
        elif isinstance(max_uniques, float):
            m = int(arr.size * min(max_uniques, 1.0))
        uniques, ix = numba_unique(arr, m)
        result = np.array([func(x) for x in uniques])
        return result[ix].reshape(shape)
    return func_vect

nb_unique = vectorize_nb_unique()(pure)
nb_unique.__name__ = 'nb_unique'

cy_unique()

%%cython -c-O3 -c-march=native -a
#cython: language_level=3, boundscheck=False, wraparound=False, initializedcheck=False, cdivision=True, infer_types=True
import numpy as np
import cython as cy

cimport cython as ccy
cimport numpy as cnp


ctypedef fused arr_t:
    cnp.uint16_t
    cnp.uint32_t
    cnp.uint64_t
    cnp.int16_t
    cnp.int32_t
    cnp.int64_t
    cnp.float32_t
    cnp.float64_t
    cnp.complex64_t
    cnp.complex128_t


def sort_numpy(arr_t[:] a):
    np.asarray(a).sort()


cpdef cnp.int64_t cython_unique(
        arr_t[:] arr,
        arr_t[::1] uniques,
        cnp.int64_t[:] ix):
    cdef size_t size = arr.size
    cdef arr_t x
    cdef cnp.int64_t i, j, k, num_uniques
    j = 0
    for i in range(size):
        found = False
        for k in range(j):
            if arr[i] == uniques[k]:
                found = True
                break
        if not found:
            uniques[j] = arr[i]
            j += 1            
    sort_numpy(uniques[:j])
    num_uniques = j
    for j in range(num_uniques):
        x = uniques[j]
        for i in range(size):
            if arr[i] == x:
                ix[i] = j
    return num_uniques

import functools
import numpy as np
import flyingcircus as fc


@fc.base.parametric
def vectorize_cy_unique(func, max_uniques=0):
    @functools.wraps(func)
    def func_vect(arr):
        shape = arr.shape
        arr = arr.ravel()
        if max_uniques <= 0:
            m = arr.size
        elif isinstance(max_uniques, int):
            m = min(max_uniques, arr.size)
        elif isinstance(max_uniques, float):
            m = int(arr.size * min(max_uniques, 1.0))
        ix = np.empty(arr.size, dtype=np.int64)
        uniques = np.empty(m, dtype=arr.dtype)
        num_uniques = cy_uniques(arr, uniques, ix)
        uniques = uniques[:num_uniques]
        result = np.array([func(x) for x in uniques])
        return result[ix].reshape(shape)
    return func_vect

cy_unique = vectorize_cy_unique()(pure)
cy_unique.__name__ = 'cy_unique'

cached_dict()

import functools
import numpy as np


def vectorize_cached_dict(func):
    @functools.wraps(func)
    def func_vect(arr):
        result = np.empty_like(arr.ravel())
        cache = {}
        for i, x in enumerate(arr.ravel()):
            if x not in cache:
                cache[x] = func(x)
            result[i] = cache[x]
        return result.reshape(arr.shape)
    return func_vect

cached_dict = vectorize_cached_dict(pure)
cached_dict.__name__ = 'cached_dict'

cached_dict_cy()

%%cython -c-O3 -c-march=native -a
#cython: language_level=3, boundscheck=False, wraparound=False, initializedcheck=False, cdivision=True, infer_types=True
import numpy as np
import cython as cy

cimport cython as ccy
cimport numpy as cnp


ctypedef fused arr_t:
    cnp.uint16_t
    cnp.uint32_t
    cnp.uint64_t
    cnp.int16_t
    cnp.int32_t
    cnp.int64_t
    cnp.float32_t
    cnp.float64_t
    cnp.complex64_t
    cnp.complex128_t

ctypedef fused result_t:
    cnp.uint16_t
    cnp.uint32_t
    cnp.uint64_t
    cnp.int16_t
    cnp.int32_t
    cnp.int64_t
    cnp.float32_t
    cnp.float64_t
    cnp.complex64_t
    cnp.complex128_t


cpdef void apply_cached_dict_cy(arr_t[:] arr, result_t[:] result, object func):
    cdef size_t size = arr.size
    cdef size_t i
    cdef dict cache = {}
    cdef arr_t x
    cdef result_t y
    for i in range(size):
        x = arr[i]
        if x not in cache:
            y = func(x)
            cache[x] = y
        else:
            y = cache[x]
        result[i] = y

import functools
import flyingcircus as fc


@fc.base.parametric
def vectorize_cached_dict_cy(func, dtype=None):
    @functools.wraps(func)
    def func_vect(arr):
        nonlocal dtype
        shape = arr.shape
        arr = arr.ravel()
        result = np.empty_like(arr) if dtype is None else np.empty(arr.shape, dtype=dtype)
        apply_cached_dict_cy(arr, result, func)
        return np.reshape(result, shape)
    return func_vect

cached_dict_cy = vectorize_cached_dict_cy()(pure)
cached_dict_cy.__name__ = 'cached_dict_cy'

cached_arr_cy()

%%cython -c-O3 -c-march=native -a
#cython: language_level=3, boundscheck=False, wraparound=False, initializedcheck=False, cdivision=True, infer_types=True
import numpy as np
import cython as cy

cimport cython as ccy
cimport numpy as cnp


ctypedef fused arr_t:
    cnp.uint16_t
    cnp.uint32_t
    cnp.uint64_t
    cnp.int16_t
    cnp.int32_t
    cnp.int64_t
    cnp.float32_t
    cnp.float64_t
    cnp.complex64_t
    cnp.complex128_t

ctypedef fused result_t:
    cnp.uint16_t
    cnp.uint32_t
    cnp.uint64_t
    cnp.int16_t
    cnp.int32_t
    cnp.int64_t
    cnp.float32_t
    cnp.float64_t
    cnp.complex64_t
    cnp.complex128_t


cpdef void apply_cached_arr_cy(
        arr_t[:] arr,
        result_t[:] result,
        object func,
        arr_t[:] uniques,
        result_t[:] func_uniques):
    cdef size_t i
    cdef size_t j
    cdef size_t k
    cdef size_t size = arr.size
    j = 0
    for i in range(size):
        found = False
        for k in range(j):
            if arr[i] == uniques[k]:
                found = True
                break
        if not found:
            uniques[j] = arr[i]
            func_uniques[j] = func(arr[i])
            result[i] = func_uniques[j]
            j += 1
        else:
            result[i] = func_uniques[k]

import functools
import numpy as np
import flyingcircus as fc


@fc.base.parametric
def vectorize_cached_arr_cy(func, dtype=None, max_uniques=None):
    @functools.wraps(func)
    def func_vect(arr):
        nonlocal dtype, max_uniques
        shape = arr.shape
        arr = arr.ravel()
        result = np.empty_like(arr) if dtype is None else np.empty(arr.shape, dtype=dtype)
        if max_uniques is None or max_uniques <= 0:
            max_uniques = arr.size
        elif isinstance(max_uniques, int):
            max_uniques = min(max_uniques, arr.size)
        elif isinstance(max_uniques, float):
            max_uniques = int(arr.size * min(max_uniques, 1.0))
        uniques = np.empty(max_uniques, dtype=arr.dtype)
        func_uniques = np.empty_like(arr) if dtype is None else np.empty(max_uniques, dtype=dtype)
        apply_cached_arr_cy(arr, result, func, uniques, func_uniques)
        return np.reshape(result, shape)
    return func_vect

cached_arr_cy = vectorize_cached_arr_cy()(pure)
cached_arr_cy.__name__ = 'cached_arr_cy'

Notes

The meta-decorator @parametric (inspired from here and available in FlyingCircus as flyingcircus.base.parametric) is defined as below:

def parametric(decorator):
    @functools.wraps(decorator)
    def _decorator(*_args, **_kws):
        def _wrapper(func):
            return decorator(func, *_args, **_kws)

        return _wrapper

    return _decorator

Numba would not be able to handle single-pass methods more efficiently than regular Python code because passing an arbitrary callable would require Python object support enabled, thereby excluding fast JIT looping.

Cython has some limitation in that you would need to specify the expected result data type. You could also tentatively guess it from the input data type, but that is not really ideal.

Some implementation requiring a temporary storage were implemented for simplicity using a static NumPy array. It would be possible to improve these implementations with dynamic arrays in C++, for example, without much loss in speed, but much improved memory footprint.

Benchmarks

Slow function with only 10 unique values (less than ~0.05%)

(This is essentially the use-case of the original post).

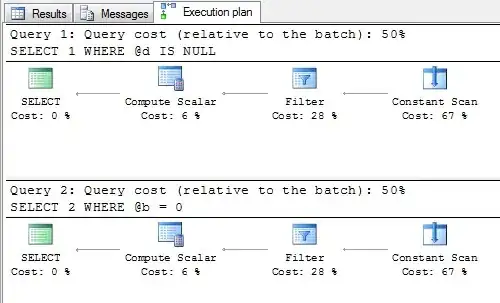
Fast function with ~0.05% unique values

Fast function with ~10% unique values

Fast function with ~20% unique values

The full benchmark code (based on this template) is available here.

Discussion and Conclusion

The fastest approach will depend on both N and U. For slow functions, all cached approaches are faster than just vectorized(). This result should be taken with a grain of salt of course, because the slow function tested here is ~4 orders of magnitude slower than the fast function, and such slow analytical functions are not really too common. If the function can be written in vectorized form right away, that is by far and large the fastest approach.

In general, cached_dict_cy() is quite memory efficient and faster than vectorized() (even for fast functions) as long as U / N is ~20% or less. Its major drawback is that requires Cython, which is a somewhat complex dependency and it would also require specifying the result data type. The np_unique() approach is faster than vectorized() (even for fast functions) as long as U / N is ~10% or less. The pd_unique() approach is competitive only for very small U and slow func.

For very small U, hashing is marginally less beneficial and cached_arr_cy() is the fastest approach.

Answer 3

After poking around a bit, here is one approach that uses pandas.unique (based on hashing) instead of numpy.unique (based on sorting).

import pandas as pd

def vectorize_with_pandas(f):
    @wraps(f)
    def f_vec(arr):
        uniques = np.sort(pd.unique(arr.ravel()))
        f_range = np.array([f(x) for x in uniques])
        return f_range[
            np.searchsorted(uniques, arr.ravel())
            ].reshape(arr.shape)
    return f_vec

Giving the following performance boost:

N = 1_000_000
np.random.seed(0)
arr = np.random.randint(0, 10, size=(N, 2)).astype(float)

@vectorize_with_pandas
def pandas_vectorize(x):
    sleep(0.001)
    return x

In [33]: %timeit pure_vectorize(arr)                                         
152 ms ± 2.34 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)

In [34]: %timeit pandas_vectorize(arr)                                       
76.8 ms ± 582 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)

Also, based on a suggestion by Warren Weckesser, you could go even faster if arr is an array of small integers, e.g. uint8. For example,

def unique_uint8(arr):
    q = np.zeros(256, dtype=int)
    q[arr.ravel()] = 1
    return np.nonzero(q)[0]


def vectorize_uint8(f):
    @wraps(f)
    def f_vec(arr):
        uniques = unique_uint8(arr)
        f_range = np.array([f(x) for x in uniques])
        return f_range[
            np.searchsorted(uniques, arr.ravel())
            ].reshape(arr.shape)
    return f_vec

Answer 4

The following decorator is:

• 10x faster than your usual_vectorize
• 10x slower than your vectorize_pure
• not doing any sorting (to the best of my knowledge)
• using numpy vectorized operations

Code:

def vectorize_pure2(f):
    @wraps(f)
    def f_vec(arr):
        tups = [tuple(x) for x in arr]
        tups_rows = dict(zip(tups, arr))
        new_arr = np.ndarray(arr.shape)
        for row in tups_rows.values():
            row_ixs = (arr == row).all(axis=1)
            new_arr[row_ixs] = f(row)
        return new_arr
    return f_vec

Performance:

@vectorize_pure2
def pure_vectorize2(x):
    sleep(0.001)
    return x

In [49]: %timeit pure_vectorize2(arr)
135 ms ± 879 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)

Some credit due this answer: https://stackoverflow.com/a/16992881/4960855