How to efficiently set matrix's minor in Mathematica?

Question

While looking at the belisarius's question about generation of non-singular integer matrices with uniform distribution of its elements, I was studying a paper by Dana Randal, "Efficient generation of random non-singular matrices". The algorithm proposed is recursive, and involves generating a matrix of lower dimension and assigning it to a given minor. I used combinations of Insert and Transpose to do it, but there are must be more efficient ways of doing it. How would you do it?

The following is the code:

Clear[Gen];
Gen[p_, 1] := {{{1}}, RandomInteger[{1, p - 1}, {1, 1}]};
Gen[p_, n_] := Module[{v, r, aa, tt, afr, am, tm},
  While[True,
   v = RandomInteger[{0, p - 1}, n];
   r = LengthWhile[v, # == 0 &] + 1;
   If[r <= n, Break[]]
   ];
  afr = UnitVector[n, r];
  {am, tm} = Gen[p, n - 1];
  {Insert[
    Transpose[
     Insert[Transpose[am], RandomInteger[{0, p - 1}, n - 1], r]], afr,
     1], Insert[
    Transpose[Insert[Transpose[tm], ConstantArray[0, n - 1], r]], v, 
    r]}
  ]

NonSingularRandomMatrix[p_?PrimeQ, n_] := Mod[Dot @@ Gen[p, n], p]

It does generate a non-singular matrix, and has uniform distribution of matrix elements, but requires p to be prime:

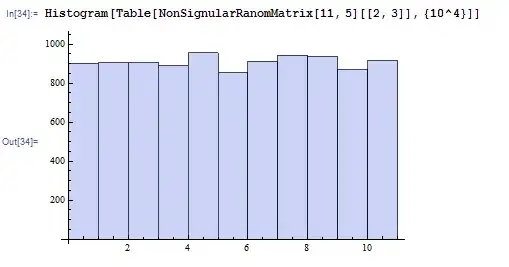
The code is also not every efficient, which is, I suspect due to my inefficient matrix constructors:

In[10]:= Timing[NonSingularRandomMatrix[101, 300];]

Out[10]= {0.421, Null}

---

EDIT So let me condense my question. The minor matrix of a given matrix m can be computed as follows:

MinorMatrix[m_?MatrixQ, {i_, j_}] := 
 Drop[Transpose[Drop[Transpose[m], {j}]], {i}]

It is the original matrix with i-th row and j-th column deleted.

I now need to create a matrix of size n by n that will have the given minor matrix mm at position {i,j}. What I used in the algorithm was:

ExpandMinor[minmat_, {i_, j_}, v1_, 
   v2_] /; {Length[v1] - 1, Length[v2]} == Dimensions[minmat] := 
 Insert[Transpose[Insert[Transpose[minmat], v2, j]], v1, i]

Example:

In[31]:= ExpandMinor[
 IdentityMatrix[4], {2, 3}, {1, 2, 3, 4, 5}, {2, 3, 4, 4}]

Out[31]= {{1, 0, 2, 0, 0}, {1, 2, 3, 4, 5}, {0, 1, 3, 0, 0}, {0, 0, 4,
   1, 0}, {0, 0, 4, 0, 1}}

I am hoping this can be done more efficiently, which is what I am soliciting in the question.

---

Per blisarius's suggestion I looked into implementing ExpandMinor via ArrayFlatten.

Clear[ExpandMinorAlt];
ExpandMinorAlt[m_, {i_ /; i > 1, j_}, v1_, 
   v2_] /; {Length[v1] - 1, Length[v2]} == Dimensions[m] :=
 ArrayFlatten[{
   {Part[m, ;; i - 1, ;; j - 1], Transpose@{v2[[;; i - 1]]}, 
    Part[m, ;; i - 1, j ;;]},
   {{v1[[;; j - 1]]}, {{v1[[j]]}}, {v1[[j + 1 ;;]]}},
   {Part[m, i ;;, ;; j - 1], Transpose@{v2[[i ;;]]}, Part[m, i ;;, j ;;]}
   }]

ExpandMinorAlt[m_, {1, j_}, v1_, 
   v2_] /; {Length[v1] - 1, Length[v2]} == Dimensions[m] :=
 ArrayFlatten[{
   {{v1[[;; j - 1]]}, {{v1[[j]]}}, {v1[[j + 1 ;;]]}},
   {Part[m, All, ;; j - 1], Transpose@{v2}, Part[m, All, j ;;]}
   }]

In[192]:= dim = 5;
mm = RandomInteger[{-5, 5}, {dim, dim}];
v1 = RandomInteger[{-5, 5}, dim + 1];
v2 = RandomInteger[{-5, 5}, dim];

In[196]:= 
Table[ExpandMinor[mm, {i, j}, v1, v2] == 
    ExpandMinorAlt[mm, {i, j}, v1, v2], {i, dim}, {j, dim}] // 
  Flatten // DeleteDuplicates

Out[196]= {True}

Answer 1

It took me a while to get here, but since I spent a good part of my postdoc generating random matrices, I could not help it, so here goes. The main inefficiency in the code comes from the necessity to move matrices around (copy them). If we could reformulate the algorithm so that we only modify a single matrix in place, we could win big. For this, we must compute the positions where the inserted vectors/rows will end up, given that we will typically insert in the middle of smaller matrices and thus shift the elements. This is possible. Here is the code:

gen = Compile[{{p, _Integer}, {n, _Integer}},
 Module[{vmat = Table[0, {n}, {n}],
    rs = Table[0, {n}],(* A vector of r-s*)
    amatr = Table[0, {n}, {n}],
    tmatr = Table[0, {n}, {n}],
    i = 1,
    v = Table[0, {n}],
    r = n + 1,
    rsc = Table[0, {n}], (* recomputed r-s *)
    matstarts = Table[0, {n}], (* Horizontal positions of submatrix starts at a given step *)    
    remainingShifts = Table[0, {n}] 
      (* 
      ** shifts that will be performed after a given row/vector insertion, 
      ** and can affect the real positions where the elements will end up
      *)
},
(* 
 ** Compute the r-s and vectors v all at once. Pad smaller 
 ** vectors v with zeros to fill a rectangular matrix
*)
For[i = 1, i <= n, i++,
 While[True,
  v = RandomInteger[{0, p - 1}, i];
  For[r = 1, r <= i && v[[r]] == 0, r++];
  If[r <= i,
   vmat[[i]] = PadRight[v, n];
   rs[[i]] = r;
   Break[]]
  ]];
 (* 
 ** We must recompute the actual r-s, since the elements will 
 ** move due to subsequent column insertions. 
 ** The code below repeatedly adds shifts to the 
 ** r-s on the left, resulting from insertions on the right. 
 ** For example, if vector of r-s 
 ** is {1,2,1,3}, it will become {1,2,1,3}->{2,3,1,3}->{2,4,1,3}, 
 ** and the end result shows where
 ** in the actual matrix the columns (and also rows for the case of 
 ** tmatr) will be inserted 
 *)
 rsc = rs;
 For[i = 2, i <= n, i++,
  remainingShifts = Take[rsc, i - 1];
  For[r = 1, r <= i - 1, r++,
   If[remainingShifts[[r]] == rsc[[i]],
     Break[]
   ]
  ];
  If[ r <= n,
    rsc[[;; i - 1]] += UnitStep[rsc[[;; i - 1]] - rsc[[i]]]
  ]
 ];
 (* 
  ** Compute the starting left positions of sub-
  ** matrices at each step (1x1,2x2,etc)
 *)
 matstarts = FoldList[Min, First@rsc, Rest@rsc];
 (* Initialize matrices - this replaces the recursion base *)
 amatr[[n, rsc[[1]]]] = 1;
 tmatr[[rsc[[1]], rsc[[1]]]] = RandomInteger[{1, p - 1}];
 (* Repeatedly perform insertions  - this replaces recursion *)
 For[i = 2, i <= n, i++,
  amatr[[n - i + 2 ;; n, rsc[[i]]]] = RandomInteger[{0, p - 1}, i - 1];
  amatr[[n - i + 1, rsc[[i]]]] = 1;
  tmatr[[n - i + 2 ;; n, rsc[[i]]]] = Table[0, {i - 1}];
  tmatr[[rsc[[i]], 
    Fold[# + 1 - Unitize[# - #2] &, 
       matstarts[[i]] + Range[0, i - 1], Sort[Drop[rsc, i]]]]] = 
            vmat[[i, 1 ;; i]];    
 ];
 {amatr, tmatr}
 ], 
 {{FoldList[__], _Integer, 1}}, CompilationTarget -> "C"];

NonSignularRanomMatrix[p_?PrimeQ, n_] := Mod[Dot @@ Gen[p, n],p];
NonSignularRanomMatrixAlt[p_?PrimeQ, n_] := Mod[Dot @@ gen[p, n],p];

Here is the timing for the large matrix:

In[1114]:= gen [101, 300]; // Timing

Out[1114]= {0.078, Null}

For the histogram, I get the identical plots, and the 10-fold efficiency boost:

In[1118]:= 
  Histogram[Table[NonSignularRanomMatrix[11, 5][[2, 3]], {10^4}]]; // Timing

Out[1118]= {7.75, Null} 

In[1119]:= 
 Histogram[Table[NonSignularRanomMatrixAlt[11, 5][[2, 3]], {10^4}]]; // Timing

Out[1119]= {0.687, Null}

I expect that upon careful profiling of the above compiled code, one could further improve the performance. Also, I did not use runtime Listable attribute in Compile, while this should be possible. It may also be that the parts of the code which perform assignment to minors are generic enough so that the logic can be factored out of the main function - I did not investigate that yet.

Answer 2

For the first part of your question (which I hope I understand properly) can MinorMatrix be written as follows?

MinorMatrixAlt[m_?MatrixQ, {i_, j_}] := Drop[mat, {i}, {j}]