How to find all possible "continuous" paths of a matrix / network / graph in R

Question

I am interested in determining all of the possible "continuous" paths of an NxN matrix in R and returning their result. By "continuous" I mean that we can travel without lifting up your pencil/digit. That is, we can move up, down, left, right, or diagonally.

To make this concrete, let's use a 3x3 matrix example:

mat_3x3 <- matrix(LETTERS[1:9], ncol = 3, byrow = TRUE)
mat_3x3
#      [,1] [,2] [,3]
# [1,] "A"  "B"  "C" 
# [2,] "D"  "E"  "F" 
# [3,] "G"  "H"  "I" 

This means we have the following valid and invalid paths:

Some considerations:

• The start position does not need to be position A (1, 1).
• We cannot "double-back" or touch the same cell multiple times.
• Short paths are possible (e.g. A -> B -> C is a valid path; likewise, A -> E -> I) -- that is, we do not need to pass through all the nodes.

If there is a package or concept that facilitates, please advise (most of the graph traversal packages I have seen are more "graph" than "matrix"). I'd imagine dynamic programming or recursion is probably of use here, but I am not sure how to start.

---

I believe the answer to the 2X2 case could be 60 per the following solution for one cell with paths = 15; 15 * 4 = 60:

However, things escalate quickly for a 3x3, 4x4, case...no longer just corners, the addition of "center" squares, etc...

---

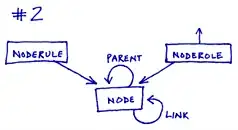
If we think about this problem as more of a graph or network, we have the following for the 3X3 case:

Why though? I am just genuinely interested in this problem and find it fascinating. I'd like to understand how to program it in R, but I'd consider other answers if they exist (then perhaps translate them to R). It started as a thought experiment thinking about a "game" where you you slide your finger on a touch screen to create words from the string of characters. Rather than minimum cost, we'd like to maximize score -- using a Z scores more points than an E like in Scrabble, etc. But I suppose this has interesting applications in social networks, graph theory, transportation optimization, and other domains.

Answer 1

This will work any size matrix (limited by hardware) and does not require the matrix to be rectangular e.g. 3 x 4. It builds a validity matrix that has all of the original matrix positions as columns and the row will return TRUE if it's a valid move and FALSE if not. I didn't validate all results, but the spot checks I did worked.

library(gtools)

# convert matrix to numbers to reference by position
m <- matrix(seq_along(mat_3x3), ncol = ncol(mat_3x3))

# create blank matrix that is used to see if it is a valid move
mLength <- length(m)
mValid <- matrix(rep(FALSE, mLength ^ 2), ncol = mLength)

# create index to generate validity matrix
xIndex <- seq_len(ncol(m))
yIndex <- seq_len(nrow(m))

# wrap with NA to prevent out of bounds
mBounds <- rbind(NA, cbind(NA, m, NA), NA)

# set validity matrix TRUE if returns a value that is not NA
mValid[cbind(as.vector(mBounds[yIndex + 1, xIndex + 2]), seq_len(mLength))] <- TRUE
mValid[cbind(as.vector(mBounds[yIndex + 2, xIndex + 2]), seq_len(mLength))] <- TRUE
mValid[cbind(as.vector(mBounds[yIndex + 2, xIndex + 1]), seq_len(mLength))] <- TRUE
mValid[cbind(as.vector(mBounds[yIndex + 2, xIndex    ]), seq_len(mLength))] <- TRUE
mValid[cbind(as.vector(mBounds[yIndex + 1, xIndex    ]), seq_len(mLength))] <- TRUE
mValid[cbind(as.vector(mBounds[yIndex    , xIndex    ]), seq_len(mLength))] <- TRUE
mValid[cbind(as.vector(mBounds[yIndex    , xIndex + 1]), seq_len(mLength))] <- TRUE
mValid[cbind(as.vector(mBounds[yIndex    , xIndex + 2]), seq_len(mLength))] <- TRUE

# define function to check if provided sequence is valid
validate <- function(x) {
  all(mValid[cbind(x[-1], x[-length(x)])])
}

# generate all permutations
p1 <- permutations(mLength, mLength)
p2 <- apply(p1, 1, validate)
p2 <- p1[p2, ]

# some results
> mat_3x3[p2[1, ]]
[1] "A" "D" "G" "E" "B" "C" "F" "H" "I"

> mat_3x3[p2[531, ]]
[1] "C" "E" "H" "G" "D" "A" "B" "F" "I"

To generate other sequences that do not use all letters would require changing the permutations function above to limit the target vector length:

p1 <- permutations(mLength, mLength - 1)
p2 <- apply(p1, 1, validate)
p2 <- p1[p2, ]

> mat_3x3[p2[1701, ]]
[1] "C" "F" "B" "D" "G" "E" "I" "H"

Using combinat::permn to use the validate function while building the permutations.

library(combinat)
p <- list()
pTemp <- permn(mLength, function(x) x[validate(x)])
p[[mLength]] <- pTemp[lengths(pTemp) > 0]

# breaking all paths that use every option into smaller pieces to find shorter paths
for (i in seq_len(mLength)[-mLength]) {
  pTemp <- lapply(p[[mLength]], function(x, y) embed(rev(x), length(x) - y), y = i)
  p[[mLength - i]] <- unique(do.call(rbind, pTemp))
}

# total number of paths
sum(unlist(lapply(p, nrow)), length(p[[mLength]]))