Note: I have already accepted the answer from Izaak van Dongen above. This answer is to provide context for the question for those that may be interested.
I was reading a book on SDEs and I asked a question on the measure theory presentation of probability space. There are a large number of structural definitions involved. I wanted to use SymPy to organize them and present the type signatures in something mimicking Axiom style.
To do this pleasantly in Python 3 and SymPy I needed a few things:
- A way of dynamically enforcing function signatures.
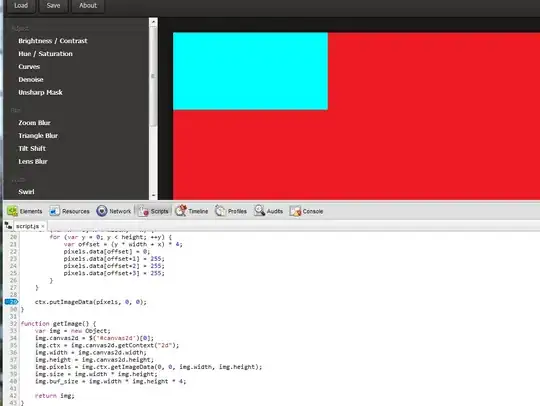
- A way of pretty-printing complex algebraic type signatures (this question).
I started implementing the definitions. To check that they were organized correctly, I asked
With that in hand, and the above solution for the pretty-printing, the following few definitions give the style of my solution (without quoting the whole thing which is about 85 definitions):
import sympy as sp # I am at version 1.6.1
from typen import strict_type_hints, enforce_type_hints
from traits.api import Array, Either, Enum, Instance, Int, Str, Tuple
class Concept(sp.Expr):
def __init__(self, name, value):
self.name = name
self.value = value
def _latex(self, printer=None):
return f"{self.name}:\\ \\text{{{self.__class__.__name__}}}"
class NonemptySet(Concept):
def __init__(self, name, value):
if value==sp.S.EmptySet:
raise ValueError("Set must not be empty")
super().__init__(name, value)
def _latex(self, printer=None):
return self.name
class Reals(NonemptySet):
@strict_type_hints
def __init__(self):
self.name = sp.symbols('\\Re')
super().__init__(self.name,sp.Reals)
def _latex(self, printer=None):
return self.name
class SampleSpace (NonemptySet):
pass
class Algebra(NonemptySet):
@strict_type_hints
def __init__(self,
name: sp.Symbol,
Ω: SampleSpace,
A: Either(NonemptySet, sp.Symbol)):
self.Ω=Ω
super().__init__(name, A)
def _latex(self, printer=None):
math=str(self.name).replace('$','')
math2 = self.Ω._latex(printer)
return f"{math}:\\ \\text{{{self.__class__.__name__} on }} ({math2})"
class Algebra(Algebra):
@strict_type_hints
def __init__(self, name: sp.Symbol, Ω: SampleSpace, A: Algebra):
self.Ω=Ω
super().__init__(name, Ω, A)
class EventSpace(Algebra):
@strict_type_hints
def __init__(self, name: sp.Symbol, Ω: SampleSpace, A: Algebra):
super().__init__(name, Ω, A)
class AdditiveFunction(Concept):
@strict_type_hints
def __init__(self,
name: sp.core.function.UndefinedFunction,
Ω: SampleSpace,
A: Algebra,
f: sp.core.function.UndefinedFunction):
self.Ω = Ω
self.A = A
super().__init__(name, f)
def _latex(self, printer=None):
math2 = self.A._latex(printer)
return f"{self.name}: {self.A.name} \\to \\Re \\ \\text{{{self.__class__.__name__} on }} {math2}"
and so on. Any comments or suggestions on a more "SymPy-thonic" way of improving the above sketch would be greatly appreciated.