I have a 3D planar (all vertices lie in some plane) polygon with vertices: [(x1, y1, z1) ... (x1, y1, z1)].
I would like to transform this polygon so that I'm viewing it orthographically (as if I'm looking at it straight on).
How can this be done in Python?
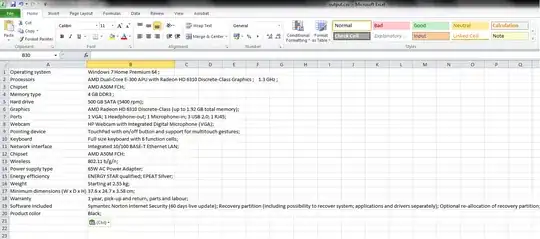
I assume you have no information except for vertex coordinates.
Take three non-collinear (perhaps consequent) vertices C, A, B. Calculate normalized vector (divide by vector length)
b = (B - A) / |B - A|
then normal vector (using vector/cross multiplication)
N = b.cross.(A-C) and normalize it
un = N / |N|
and another unit vector in polygon plane
v = b.cross.n
Now we want find such matrix of affine transformations, that transforms vertex A into point (0,0,0), edge AB will be collinear with OX axis, normal will be collinear with OZ axis, vector q will be collinear with OY axis. This all means that rotated polygon will lie in OXY plane.
Mathematically: points A, u=A+b, v=A+q, n=A+un should be transformed in quadruplet (0,0,0), (1,0,0), (0,1,0), (0,0,1). In matrix form
[Ax ux vx nx] [0 1 0 0]
M * [Ay uy vy ny] = [0 0 1 0]
[Az uz vz nz] [0 0 0 1]
[1 1 1 1 ] [1 1 1 1]
or
M * S = D
Using matrix inverse
M * S * Sinv = D * Sinv
and finally
M = D * Sinv
So calculate matrix M and multiply it with every vertex coordinates. New coordinates should have zero Z-component (or very small due to numerical errors).
You can perform all described operations with numpy library with a little code
Quick-made implementation in plain Python for reference
import math
def calcMatrix(ax, bx, cx, ay, by, cy, az, bz, cz):
ux, uy, uz = bx - ax, by - ay, bz - az
mag = math.sqrt(ux*ux+uy*uy +uz*uz)
ux, uy, uz = ux / mag, uy / mag, uz / mag
Cx, Cy, Cz = ax - cx, ay - cy, az - cz
nx, ny, nz = uy * Cz - uz * Cy, uz * Cx - ux * Cz, ux * Cy - uy * Cx
mag = math.sqrt(nx*nx+ny*ny+nz*nz)
nx, ny, nz = nx / mag, ny / mag, nz / mag
vx, vy, vz = uy * nz - uz * ny, uz * nx - ux * nz, ux * ny - uy * nx
denom = 1.0 / (ux*ux+uy*uy + uz*uz)
M = [[0.0]*4 for _ in range(4)]
M[3][3] = 1.0
M[0][0] = denom*(ux)
M[0][1] = denom*(uy)
M[0][2] = denom*(uz)
M[0][3] = denom*(-ax*ux-ay*uy+az*uz)
M[1][0] = denom*(vx)
M[1][1] = denom*(vy)
M[1][2] = denom*(vz)
M[1][3] = -denom*(ax*vx-ay*vy+az*vz)
M[2][0] = denom*(nx)
M[2][1] = denom*(ny)
M[2][2] = denom*(nz)
M[2][3] = denom*(-ax*nx-ay*ny+az*nz)
return M
def mult(M, vec):
res = [0]*4
for k in range(4):
for i in range(4):
res[k] += M[k][i] * vec[i]
return res
#test corners and middle point
M = calcMatrix(1, 0, 0, 0, 1, 0, 0, 0, 1)
#print(M)
p = [1, 0, 0, 1]
print(mult(M, p))
p = [0, 1, 0, 1]
print(mult(M, p))
p = [0, 0, 1, 1]
print(mult(M, p))
p = [1/3, 1/3, 1/3, 1]
print(mult(M, p))
test results:
[0.0, 0.0, 0.0, 1.0]
[1.4142135623730951, 0.0, 0.0, 1.0]
[0.7071067811865476, 1.2247448713915892, 0.0, 1.0]
[0.7071067811865476, 0.4082482904638631, 1.1102230246251565e-16, 1.0]
Find a normal n to the polygon, by means of a cross-product between two non-parallel sides. Take the cross-product of n with a vertical vector, to get an horizontal vector u. Then take the cross product of n and u to get v, and normalize the vectors. u and v are parallel to the plane of the polygon and orthogonal to each other.
Finally, for every vertex p compute the 2D coordinates (p.u, p.v) which show you the polygon in its plane.
numpy supplies the cross and dot vector functions. Also linalg.norm (or sqrt(dot(v, v))).
Here's a robust approach using NumPy (project(); the rest is test code).
import numpy
import scipy.spatial
def project(x):
# Center the plane on the origin
x = x - numpy.mean(x, axis=0)
# Compute the Singular Value Decomposition
u, s, v = numpy.linalg.svd(x)
# Return the top two principal components
return u[:, :2] @ numpy.diag(s[:2])
def test():
n = 10
x = (numpy.random.rand(n, 2) @ numpy.random.rand(2, 3)) + numpy.random.rand(3)
y = project(x)
print(x.shape, y.shape)
print(
numpy.max(
numpy.abs(
scipy.spatial.distance_matrix(x, x)
- scipy.spatial.distance_matrix(y, y)
)
)
)
if __name__ == "__main__":
test()
Sample output:
(10, 3) (10, 2)
5.551115123125783e-16
