Shortest distance between a point and a line segment

Question

I need a basic function to find the shortest distance between a point and a line segment. Feel free to write the solution in any language you want; I can translate it into what I'm using (Javascript).

EDIT: My line segment is defined by two endpoints. So my line segment AB is defined by the two points A (x1,y1) and B (x2,y2). I'm trying to find the distance between this line segment and a point C (x3,y3). My geometry skills are rusty, so the examples I've seen are confusing, I'm sorry to admit.

Answer 1

Eli, the code you've settled on is incorrect. A point near the line on which the segment lies but far off one end of the segment would be incorrectly judged near the segment. Update: The incorrect answer mentioned is no longer the accepted one.

Here's some correct code, in C++. It presumes a class 2D-vector class vec2 {float x,y;}, essentially, with operators to add, subract, scale, etc, and a distance and dot product function (i.e. x1 x2 + y1 y2).

float minimum_distance(vec2 v, vec2 w, vec2 p) {
  // Return minimum distance between line segment vw and point p
  const float l2 = length_squared(v, w);  // i.e. |w-v|^2 -  avoid a sqrt
  if (l2 == 0.0) return distance(p, v);   // v == w case
  // Consider the line extending the segment, parameterized as v + t (w - v).
  // We find projection of point p onto the line. 
  // It falls where t = [(p-v) . (w-v)] / |w-v|^2
  // We clamp t from [0,1] to handle points outside the segment vw.
  const float t = max(0, min(1, dot(p - v, w - v) / l2));
  const vec2 projection = v + t * (w - v);  // Projection falls on the segment
  return distance(p, projection);
}

EDIT: I needed a Javascript implementation, so here it is, with no dependencies (or comments, but it's a direct port of the above). Points are represented as objects with x and y attributes.

function sqr(x) { return x * x }
function dist2(v, w) { return sqr(v.x - w.x) + sqr(v.y - w.y) }
function distToSegmentSquared(p, v, w) {
  var l2 = dist2(v, w);
  if (l2 == 0) return dist2(p, v);
  var t = ((p.x - v.x) * (w.x - v.x) + (p.y - v.y) * (w.y - v.y)) / l2;
  t = Math.max(0, Math.min(1, t));
  return dist2(p, { x: v.x + t * (w.x - v.x),
                    y: v.y + t * (w.y - v.y) });
}
function distToSegment(p, v, w) { return Math.sqrt(distToSegmentSquared(p, v, w)); }

EDIT 2: I needed a Java version, but more important, I needed it in 3d instead of 2d.

float dist_to_segment_squared(float px, float py, float pz, float lx1, float ly1, float lz1, float lx2, float ly2, float lz2) {
  float line_dist = dist_sq(lx1, ly1, lz1, lx2, ly2, lz2);
  if (line_dist == 0) return dist_sq(px, py, pz, lx1, ly1, lz1);
  float t = ((px - lx1) * (lx2 - lx1) + (py - ly1) * (ly2 - ly1) + (pz - lz1) * (lz2 - lz1)) / line_dist;
  t = constrain(t, 0, 1);
  return dist_sq(px, py, pz, lx1 + t * (lx2 - lx1), ly1 + t * (ly2 - ly1), lz1 + t * (lz2 - lz1));
}

Here, in the function parameters, <px,py,pz> is the point in question and the line segment has the endpoints <lx1,ly1,lz1> and <lx2,ly2,lz2>. The function dist_sq (which is assumed to exist) finds the square of the distance between two points.

Answer 2

Here is the simplest complete code in Javascript.

x, y is your target point and x1, y1 to x2, y2 is your line segment.

UPDATED: fix for 0 length line problem from comments.

function pDistance(x, y, x1, y1, x2, y2) {

  var A = x - x1;
  var B = y - y1;
  var C = x2 - x1;
  var D = y2 - y1;

  var dot = A * C + B * D;
  var len_sq = C * C + D * D;
  var param = -1;
  if (len_sq != 0) //in case of 0 length line
      param = dot / len_sq;

  var xx, yy;

  if (param < 0) {
    xx = x1;
    yy = y1;
  }
  else if (param > 1) {
    xx = x2;
    yy = y2;
  }
  else {
    xx = x1 + param * C;
    yy = y1 + param * D;
  }

  var dx = x - xx;
  var dy = y - yy;
  return Math.sqrt(dx * dx + dy * dy);
}

UPDATED: Kotlin version

fun getDistance(x: Double, y: Double, x1: Double, y1: Double, x2: Double, y2: Double): Double {
    val a = x - x1
    val b = y - y1
    val c = x2 - x1
    val d = y2 - y1

    val lenSq = c * c + d * d
    val param = if (lenSq != .0) { //in case of 0 length line
        val dot = a * c + b * d
        dot / lenSq
    } else {
        -1.0
    }

    val (xx, yy) = when {
        param < 0 -> x1 to y1
        param > 1 -> x2 to y2
        else -> x1 + param * c to y1 + param * d
    }

    val dx = x - xx
    val dy = y - yy
    return hypot(dx, dy)
}

Answer 3

This is an implementation made for FINITE LINE SEGMENTS, not infinite lines like most other functions here seem to be (that's why I made this).

Implementation of theory by Paul Bourke.

Python:

def dist(x1, y1, x2, y2, x3, y3): # x3,y3 is the point
    px = x2-x1
    py = y2-y1

    norm = px*px + py*py

    u =  ((x3 - x1) * px + (y3 - y1) * py) / float(norm)

    if u > 1:
        u = 1
    elif u < 0:
        u = 0

    x = x1 + u * px
    y = y1 + u * py

    dx = x - x3
    dy = y - y3

    # Note: If the actual distance does not matter,
    # if you only want to compare what this function
    # returns to other results of this function, you
    # can just return the squared distance instead
    # (i.e. remove the sqrt) to gain a little performance

    dist = (dx*dx + dy*dy)**.5

    return dist

AS3:

public static function segmentDistToPoint(segA:Point, segB:Point, p:Point):Number
{
    var p2:Point = new Point(segB.x - segA.x, segB.y - segA.y);
    var something:Number = p2.x*p2.x + p2.y*p2.y;
    var u:Number = ((p.x - segA.x) * p2.x + (p.y - segA.y) * p2.y) / something;

    if (u > 1)
        u = 1;
    else if (u < 0)
        u = 0;

    var x:Number = segA.x + u * p2.x;
    var y:Number = segA.y + u * p2.y;

    var dx:Number = x - p.x;
    var dy:Number = y - p.y;

    var dist:Number = Math.sqrt(dx*dx + dy*dy);

    return dist;
}

Java

private double shortestDistance(float x1,float y1,float x2,float y2,float x3,float y3)
    {
        float px=x2-x1;
        float py=y2-y1;
        float temp=(px*px)+(py*py);
        float u=((x3 - x1) * px + (y3 - y1) * py) / (temp);
        if(u>1){
            u=1;
        }
        else if(u<0){
            u=0;
        }
        float x = x1 + u * px;
        float y = y1 + u * py;

        float dx = x - x3;
        float dy = y - y3;
        double dist = Math.sqrt(dx*dx + dy*dy);
        return dist;

    }

Answer 4

In my own question thread how to calculate shortest 2D distance between a point and a line segment in all cases in C, C# / .NET 2.0 or Java? I was asked to put a C# answer here when I find one: so here it is, modified from http://www.topcoder.com/tc?d1=tutorials&d2=geometry1&module=Static :

//Compute the dot product AB . BC
private double DotProduct(double[] pointA, double[] pointB, double[] pointC)
{
    double[] AB = new double[2];
    double[] BC = new double[2];
    AB[0] = pointB[0] - pointA[0];
    AB[1] = pointB[1] - pointA[1];
    BC[0] = pointC[0] - pointB[0];
    BC[1] = pointC[1] - pointB[1];
    double dot = AB[0] * BC[0] + AB[1] * BC[1];

    return dot;
}

//Compute the cross product AB x AC
private double CrossProduct(double[] pointA, double[] pointB, double[] pointC)
{
    double[] AB = new double[2];
    double[] AC = new double[2];
    AB[0] = pointB[0] - pointA[0];
    AB[1] = pointB[1] - pointA[1];
    AC[0] = pointC[0] - pointA[0];
    AC[1] = pointC[1] - pointA[1];
    double cross = AB[0] * AC[1] - AB[1] * AC[0];

    return cross;
}

//Compute the distance from A to B
double Distance(double[] pointA, double[] pointB)
{
    double d1 = pointA[0] - pointB[0];
    double d2 = pointA[1] - pointB[1];

    return Math.Sqrt(d1 * d1 + d2 * d2);
}

//Compute the distance from AB to C
//if isSegment is true, AB is a segment, not a line.
double LineToPointDistance2D(double[] pointA, double[] pointB, double[] pointC, 
    bool isSegment)
{
    double dist = CrossProduct(pointA, pointB, pointC) / Distance(pointA, pointB);
    if (isSegment)
    {
        double dot1 = DotProduct(pointA, pointB, pointC);
        if (dot1 > 0) 
            return Distance(pointB, pointC);

        double dot2 = DotProduct(pointB, pointA, pointC);
        if (dot2 > 0) 
            return Distance(pointA, pointC);
    }
    return Math.Abs(dist);
} 

I'm @SO not to answer but ask questions so I hope I don't get million down votes for some reasons but constructing critic. I just wanted (and was encouraged) to share somebody else's ideas since the solutions in this thread are either with some exotic language (Fortran, Mathematica) or tagged as faulty by somebody. The only useful one (by Grumdrig) for me is written with C++ and nobody tagged it faulty. But it's missing the methods (dot etc.) that are called.

Answer 5

For anyone interested, here's a trivial conversion of Joshua's Javascript code to Objective-C:

- (double)distanceToPoint:(CGPoint)p fromLineSegmentBetween:(CGPoint)l1 and:(CGPoint)l2
{
    double A = p.x - l1.x;
    double B = p.y - l1.y;
    double C = l2.x - l1.x;
    double D = l2.y - l1.y;

    double dot = A * C + B * D;
    double len_sq = C * C + D * D;
    double param = dot / len_sq;

    double xx, yy;

    if (param < 0 || (l1.x == l2.x && l1.y == l2.y)) {
        xx = l1.x;
        yy = l1.y;
    }
    else if (param > 1) {
        xx = l2.x;
        yy = l2.y;
    }
    else {
        xx = l1.x + param * C;
        yy = l1.y + param * D;
    }

    double dx = p.x - xx;
    double dy = p.y - yy;

    return sqrtf(dx * dx + dy * dy);
}

I needed this solution to work with MKMapPoint so I will share it in case someone else needs it. Just some minor change and this will return the distance in meters :

- (double)distanceToPoint:(MKMapPoint)p fromLineSegmentBetween:(MKMapPoint)l1 and:(MKMapPoint)l2
{
    double A = p.x - l1.x;
    double B = p.y - l1.y;
    double C = l2.x - l1.x;
    double D = l2.y - l1.y;

    double dot = A * C + B * D;
    double len_sq = C * C + D * D;
    double param = dot / len_sq;

    double xx, yy;

    if (param < 0 || (l1.x == l2.x && l1.y == l2.y)) {
        xx = l1.x;
        yy = l1.y;
    }
    else if (param > 1) {
        xx = l2.x;
        yy = l2.y;
    }
    else {
        xx = l1.x + param * C;
        yy = l1.y + param * D;
    }

    return MKMetersBetweenMapPoints(p, MKMapPointMake(xx, yy));
}

Answer 6

In F#, the distance from the point c to the line segment between a and b is given by:

let pointToLineSegmentDistance (a: Vector, b: Vector) (c: Vector) =
  let d = b - a
  let s = d.Length
  let lambda = (c - a) * d / s
  let p = (lambda |> max 0.0 |> min s) * d / s
  (a + p - c).Length

The vector d points from a to b along the line segment. The dot product of d/s with c-a gives the parameter of the point of closest approach between the infinite line and the point c. The min and max function are used to clamp this parameter to the range 0..s so that the point lies between a and b. Finally, the length of a+p-c is the distance from c to the closest point on the line segment.

Example use:

pointToLineSegmentDistance (Vector(0.0, 0.0), Vector(1.0, 0.0)) (Vector(-1.0, 1.0))

Answer 7

In Mathematica

It uses a parametric description of the segment, and projects the point into the line defined by the segment. As the parameter goes from 0 to 1 in the segment, if the projection is outside this bounds, we compute the distance to the corresponding enpoint, instead of the straight line normal to the segment.

Clear["Global`*"];
 distance[{start_, end_}, pt_] := 
   Module[{param},
   param = ((pt - start).(end - start))/Norm[end - start]^2; (*parameter. the "."
                                                       here means vector product*)

   Which[
    param < 0, EuclideanDistance[start, pt],                 (*If outside bounds*)
    param > 1, EuclideanDistance[end, pt],
    True, EuclideanDistance[pt, start + param (end - start)] (*Normal distance*)
    ]
   ];  

Plotting result:

Plot3D[distance[{{0, 0}, {1, 0}}, {xp, yp}], {xp, -1, 2}, {yp, -1, 2}]

Plot those points nearer than a cutoff distance:

Contour Plot:

Answer 8

For the lazy, here's my Objective-C port of @Grumdrig's solution above:

CGFloat sqr(CGFloat x) { return x*x; }
CGFloat dist2(CGPoint v, CGPoint w) { return sqr(v.x - w.x) + sqr(v.y - w.y); }
CGFloat distanceToSegmentSquared(CGPoint p, CGPoint v, CGPoint w)
{
    CGFloat l2 = dist2(v, w);
    if (l2 == 0.0f) return dist2(p, v);

    CGFloat t = ((p.x - v.x) * (w.x - v.x) + (p.y - v.y) * (w.y - v.y)) / l2;
    if (t < 0.0f) return dist2(p, v);
    if (t > 1.0f) return dist2(p, w);
    return dist2(p, CGPointMake(v.x + t * (w.x - v.x), v.y + t * (w.y - v.y)));
}
CGFloat distanceToSegment(CGPoint point, CGPoint segmentPointV, CGPoint segmentPointW)
{
    return sqrtf(distanceToSegmentSquared(point, segmentPointV, segmentPointW));
}

Answer 9

One line solution using arctangents:

The idea is to move A to (0, 0) and rotate triangle clockwise to make C lay on X axis, when this happen, By will be the distance.

1. a angle = Atan(Cy - Ay, Cx - Ax);
2. b angle = Atan(By - Ay, Bx - Ax);
3. AB length = Sqrt( (Bx - Ax)^2 + (By - Ay)^2 )
4. By = Sin ( bAngle - aAngle) * ABLength

C#

public double Distance(Point a, Point b, Point c)
{
    // normalize points
    Point cn = new Point(c.X - a.X, c.Y - a.Y);
    Point bn = new Point(b.X - a.X, b.Y - a.Y);

    double angle = Math.Atan2(bn.Y, bn.X) - Math.Atan2(cn.Y, cn.X);
    double abLength = Math.Sqrt(bn.X*bn.X + bn.Y*bn.Y);

    return Math.Sin(angle)*abLength;
}

One line C# (to be converted to SQL)

double distance = Math.Sin(Math.Atan2(b.Y - a.Y, b.X - a.X) - Math.Atan2(c.Y - a.Y, c.X - a.X)) * Math.Sqrt((b.X - a.X) * (b.X - a.X) + (b.Y - a.Y) * (b.Y - a.Y))

Answer 10

Hey, I just wrote this yesterday. It's in Actionscript 3.0, which is basically Javascript, though you might not have the same Point class.

//st = start of line segment
//b = the line segment (as in: st + b = end of line segment)
//pt = point to test
//Returns distance from point to line segment.  
//Note: nearest point on the segment to the test point is right there if we ever need it
public static function linePointDist( st:Point, b:Point, pt:Point ):Number
{
    var nearestPt:Point; //closest point on seqment to pt

    var keyDot:Number = dot( b, pt.subtract( st ) ); //key dot product
    var bLenSq:Number = dot( b, b ); //Segment length squared

    if( keyDot <= 0 )  //pt is "behind" st, use st
    {
        nearestPt = st  
    }
    else if( keyDot >= bLenSq ) //pt is "past" end of segment, use end (notice we are saving twin sqrts here cuz)
    {
        nearestPt = st.add(b);
    }
    else //pt is inside segment, reuse keyDot and bLenSq to get percent of seqment to move in to find closest point
    {
        var keyDotToPctOfB:Number = keyDot/bLenSq; //REM dot product comes squared
        var partOfB:Point = new Point( b.x * keyDotToPctOfB, b.y * keyDotToPctOfB );
        nearestPt = st.add(partOfB);
    }

    var dist:Number = (pt.subtract(nearestPt)).length;

    return dist;
}

Also, there's a pretty complete and readable discussion of the problem here: notejot.com

Answer 11

Here is a more complete spelling out of Grumdrig's solution. This version also returns the closest point itself.

#include "stdio.h"
#include "math.h"

class Vec2
{
public:
    float _x;
    float _y;

    Vec2()
    {
        _x = 0;
        _y = 0;
    }

    Vec2( const float x, const float y )
    {
        _x = x;
        _y = y;
    }

    Vec2 operator+( const Vec2 &v ) const
    {
        return Vec2( this->_x + v._x, this->_y + v._y );
    }

    Vec2 operator-( const Vec2 &v ) const
    {
        return Vec2( this->_x - v._x, this->_y - v._y );
    }

    Vec2 operator*( const float f ) const
    {
        return Vec2( this->_x * f, this->_y * f );
    }

    float DistanceToSquared( const Vec2 p ) const
    {
        const float dX = p._x - this->_x;
        const float dY = p._y - this->_y;

        return dX * dX + dY * dY;
    }

    float DistanceTo( const Vec2 p ) const
    {
        return sqrt( this->DistanceToSquared( p ) );
    }

    float DotProduct( const Vec2 p ) const
    {
        return this->_x * p._x + this->_y * p._y;
    }
};

// return minimum distance between line segment vw and point p, and the closest point on the line segment, q
float DistanceFromLineSegmentToPoint( const Vec2 v, const Vec2 w, const Vec2 p, Vec2 * const q )
{
    const float distSq = v.DistanceToSquared( w ); // i.e. |w-v|^2 ... avoid a sqrt
    if ( distSq == 0.0 )
    {
        // v == w case
        (*q) = v;

        return v.DistanceTo( p );
    }

    // consider the line extending the segment, parameterized as v + t (w - v)
    // we find projection of point p onto the line
    // it falls where t = [(p-v) . (w-v)] / |w-v|^2

    const float t = ( p - v ).DotProduct( w - v ) / distSq;
    if ( t < 0.0 )
    {
        // beyond the v end of the segment
        (*q) = v;

        return v.DistanceTo( p );
    }
    else if ( t > 1.0 )
    {
        // beyond the w end of the segment
        (*q) = w;

        return w.DistanceTo( p );
    }

    // projection falls on the segment
    const Vec2 projection = v + ( ( w - v ) * t );

    (*q) = projection;

    return p.DistanceTo( projection );
}

float DistanceFromLineSegmentToPoint( float segmentX1, float segmentY1, float segmentX2, float segmentY2, float pX, float pY, float *qX, float *qY )
{
    Vec2 q;

    float distance = DistanceFromLineSegmentToPoint( Vec2( segmentX1, segmentY1 ), Vec2( segmentX2, segmentY2 ), Vec2( pX, pY ), &q );

    (*qX) = q._x;
    (*qY) = q._y;

    return distance;
}

void TestDistanceFromLineSegmentToPoint( float segmentX1, float segmentY1, float segmentX2, float segmentY2, float pX, float pY )
{
    float qX;
    float qY;
    float d = DistanceFromLineSegmentToPoint( segmentX1, segmentY1, segmentX2, segmentY2, pX, pY, &qX, &qY );
    printf( "line segment = ( ( %f, %f ), ( %f, %f ) ), p = ( %f, %f ), distance = %f, q = ( %f, %f )\n",
            segmentX1, segmentY1, segmentX2, segmentY2, pX, pY, d, qX, qY );
}

void TestDistanceFromLineSegmentToPoint()
{
    TestDistanceFromLineSegmentToPoint( 0, 0, 1, 1, 1, 0 );
    TestDistanceFromLineSegmentToPoint( 0, 0, 20, 10, 5, 4 );
    TestDistanceFromLineSegmentToPoint( 0, 0, 20, 10, 30, 15 );
    TestDistanceFromLineSegmentToPoint( 0, 0, 20, 10, -30, 15 );
    TestDistanceFromLineSegmentToPoint( 0, 0, 10, 0, 5, 1 );
    TestDistanceFromLineSegmentToPoint( 0, 0, 0, 10, 1, 5 );
}

Answer 12

Couldn't resist coding it in python :)

from math import sqrt, fabs
def pdis(a, b, c):
    t = b[0]-a[0], b[1]-a[1]           # Vector ab
    dd = sqrt(t[0]**2+t[1]**2)         # Length of ab
    t = t[0]/dd, t[1]/dd               # unit vector of ab
    n = -t[1], t[0]                    # normal unit vector to ab
    ac = c[0]-a[0], c[1]-a[1]          # vector ac
    return fabs(ac[0]*n[0]+ac[1]*n[1]) # Projection of ac to n (the minimum distance)

print pdis((1,1), (2,2), (2,0))        # Example (answer is 1.414)

Ditto for fortran :)

real function pdis(a, b, c)
    real, dimension(0:1), intent(in) :: a, b, c
    real, dimension(0:1) :: t, n, ac
    real :: dd
    t = b - a                          ! Vector ab
    dd = sqrt(t(0)**2+t(1)**2)         ! Length of ab
    t = t/dd                           ! unit vector of ab
    n = (/-t(1), t(0)/)                ! normal unit vector to ab
    ac = c - a                         ! vector ac
    pdis = abs(ac(0)*n(0)+ac(1)*n(1))  ! Projection of ac to n (the minimum distance)
end function pdis


program test
    print *, pdis((/1.0,1.0/), (/2.0,2.0/), (/2.0,0.0/))   ! Example (answer is 1.414)
end program test

Answer 13

Consider this modification to Grumdrig's answer above. Many times you'll find that floating point imprecision can cause problems. I'm using doubles in the version below, but you can easily change to floats. The important part is that it uses an epsilon to handle the "slop". In addition, you'll many times want to know WHERE the intersection happened, or if it happened at all. If the returned t is < 0.0 or > 1.0, no collision occurred. However, even if no collision occurred, many times you'll want to know where the closest point on the segment to P is, and thus I use qx and qy to return this location.

double PointSegmentDistanceSquared( double px, double py,
                                    double p1x, double p1y,
                                    double p2x, double p2y,
                                    double& t,
                                    double& qx, double& qy)
{
    static const double kMinSegmentLenSquared = 0.00000001;  // adjust to suit.  If you use float, you'll probably want something like 0.000001f
    static const double kEpsilon = 1.0E-14;  // adjust to suit.  If you use floats, you'll probably want something like 1E-7f
    double dx = p2x - p1x;
    double dy = p2y - p1y;
    double dp1x = px - p1x;
    double dp1y = py - p1y;
    const double segLenSquared = (dx * dx) + (dy * dy);
    if (segLenSquared >= -kMinSegmentLenSquared && segLenSquared <= kMinSegmentLenSquared)
    {
        // segment is a point.
        qx = p1x;
        qy = p1y;
        t = 0.0;
        return ((dp1x * dp1x) + (dp1y * dp1y));
    }
    else
    {
        // Project a line from p to the segment [p1,p2].  By considering the line
        // extending the segment, parameterized as p1 + (t * (p2 - p1)),
        // we find projection of point p onto the line. 
        // It falls where t = [(p - p1) . (p2 - p1)] / |p2 - p1|^2
        t = ((dp1x * dx) + (dp1y * dy)) / segLenSquared;
        if (t < kEpsilon)
        {
            // intersects at or to the "left" of first segment vertex (p1x, p1y).  If t is approximately 0.0, then
            // intersection is at p1.  If t is less than that, then there is no intersection (i.e. p is not within
            // the 'bounds' of the segment)
            if (t > -kEpsilon)
            {
                // intersects at 1st segment vertex
                t = 0.0;
            }
            // set our 'intersection' point to p1.
            qx = p1x;
            qy = p1y;
            // Note: If you wanted the ACTUAL intersection point of where the projected lines would intersect if
            // we were doing PointLineDistanceSquared, then qx would be (p1x + (t * dx)) and qy would be (p1y + (t * dy)).
        }
        else if (t > (1.0 - kEpsilon))
        {
            // intersects at or to the "right" of second segment vertex (p2x, p2y).  If t is approximately 1.0, then
            // intersection is at p2.  If t is greater than that, then there is no intersection (i.e. p is not within
            // the 'bounds' of the segment)
            if (t < (1.0 + kEpsilon))
            {
                // intersects at 2nd segment vertex
                t = 1.0;
            }
            // set our 'intersection' point to p2.
            qx = p2x;
            qy = p2y;
            // Note: If you wanted the ACTUAL intersection point of where the projected lines would intersect if
            // we were doing PointLineDistanceSquared, then qx would be (p1x + (t * dx)) and qy would be (p1y + (t * dy)).
        }
        else
        {
            // The projection of the point to the point on the segment that is perpendicular succeeded and the point
            // is 'within' the bounds of the segment.  Set the intersection point as that projected point.
            qx = p1x + (t * dx);
            qy = p1y + (t * dy);
        }
        // return the squared distance from p to the intersection point.  Note that we return the squared distance
        // as an optimization because many times you just need to compare relative distances and the squared values
        // works fine for that.  If you want the ACTUAL distance, just take the square root of this value.
        double dpqx = px - qx;
        double dpqy = py - qy;
        return ((dpqx * dpqx) + (dpqy * dpqy));
    }
}

Answer 14

Grumdrig's C++/JavaScript implementation was very useful to me, so I have provided a Python direct port that I am using. The complete code is here.

class Point(object):
  def __init__(self, x, y):
    self.x = float(x)
    self.y = float(y)

def square(x):
  return x * x

def distance_squared(v, w):
  return square(v.x - w.x) + square(v.y - w.y)

def distance_point_segment_squared(p, v, w):
  # Segment length squared, |w-v|^2
  d2 = distance_squared(v, w) 
  if d2 == 0: 
    # v == w, return distance to v
    return distance_squared(p, v)
  # Consider the line extending the segment, parameterized as v + t (w - v).
  # We find projection of point p onto the line.
  # It falls where t = [(p-v) . (w-v)] / |w-v|^2
  t = ((p.x - v.x) * (w.x - v.x) + (p.y - v.y) * (w.y - v.y)) / d2;
  if t < 0:
    # Beyond v end of the segment
    return distance_squared(p, v)
  elif t > 1.0:
    # Beyond w end of the segment
    return distance_squared(p, w)
  else:
    # Projection falls on the segment.
    proj = Point(v.x + t * (w.x - v.x), v.y + t * (w.y - v.y))
    # print proj.x, proj.y
    return distance_squared(p, proj)

Answer 15

Here it is using Swift

    /* Distance from a point (p1) to line l1 l2 */
func distanceFromPoint(p: CGPoint, toLineSegment l1: CGPoint, and l2: CGPoint) -> CGFloat {
    let A = p.x - l1.x
    let B = p.y - l1.y
    let C = l2.x - l1.x
    let D = l2.y - l1.y
    
    let dot = A * C + B * D
    let len_sq = C * C + D * D
    var param : CGFloat = -1
    if len_sq != 0 {
        param = dot / len_sq
    }
    
    var xx, yy: CGFloat
    
    if param < 0 || (l1.x == l2.x && l1.y == l2.y) {
        xx = l1.x
        yy = l1.y
    } else if param > 1 {
        xx = l2.x
        yy = l2.y
    } else {
        xx = l1.x + param * C
        yy = l1.y + param * D
    }
    
    let dx = p.x - xx
    let dy = p.y - yy
    
    return sqrt(dx * dx + dy * dy)
}

Answer 16

I'm assuming you want to find the shortest distance between the point and a line segment; to do this, you need to find the line (lineA) which is perpendicular to your line segment (lineB) which goes through your point, determine the intersection between that line (lineA) and your line which goes through your line segment (lineB); if that point is between the two points of your line segment, then the distance is the distance between your point and the point you just found which is the intersection of lineA and lineB; if the point is not between the two points of your line segment, you need to get the distance between your point and the closer of two ends of the line segment; this can be done easily by taking the square distance (to avoid a square root) between the point and the two points of the line segment; whichever is closer, take the square root of that one.

Answer 17

And now my solution as well...... (Javascript)

It is very fast because I try to avoid any Math.pow functions.

As you can see, at the end of the function I have the distance of the line.

code is from the lib http://www.draw2d.org/graphiti/jsdoc/#!/example

/**
 * Static util function to determine is a point(px,py) on the line(x1,y1,x2,y2)
 * A simple hit test.
 * 
 * @return {boolean}
 * @static
 * @private
 * @param {Number} coronaWidth the accepted corona for the hit test
 * @param {Number} X1 x coordinate of the start point of the line
 * @param {Number} Y1 y coordinate of the start point of the line
 * @param {Number} X2 x coordinate of the end point of the line
 * @param {Number} Y2 y coordinate of the end point of the line
 * @param {Number} px x coordinate of the point to test
 * @param {Number} py y coordinate of the point to test
 **/
graphiti.shape.basic.Line.hit= function( coronaWidth, X1, Y1,  X2,  Y2, px, py)
{
  // Adjust vectors relative to X1,Y1
  // X2,Y2 becomes relative vector from X1,Y1 to end of segment
  X2 -= X1;
  Y2 -= Y1;
  // px,py becomes relative vector from X1,Y1 to test point
  px -= X1;
  py -= Y1;
  var dotprod = px * X2 + py * Y2;
  var projlenSq;
  if (dotprod <= 0.0) {
      // px,py is on the side of X1,Y1 away from X2,Y2
      // distance to segment is length of px,py vector
      // "length of its (clipped) projection" is now 0.0
      projlenSq = 0.0;
  } else {
      // switch to backwards vectors relative to X2,Y2
      // X2,Y2 are already the negative of X1,Y1=>X2,Y2
      // to get px,py to be the negative of px,py=>X2,Y2
      // the dot product of two negated vectors is the same
      // as the dot product of the two normal vectors
      px = X2 - px;
      py = Y2 - py;
      dotprod = px * X2 + py * Y2;
      if (dotprod <= 0.0) {
          // px,py is on the side of X2,Y2 away from X1,Y1
          // distance to segment is length of (backwards) px,py vector
          // "length of its (clipped) projection" is now 0.0
          projlenSq = 0.0;
      } else {
          // px,py is between X1,Y1 and X2,Y2
          // dotprod is the length of the px,py vector
          // projected on the X2,Y2=>X1,Y1 vector times the
          // length of the X2,Y2=>X1,Y1 vector
          projlenSq = dotprod * dotprod / (X2 * X2 + Y2 * Y2);
      }
  }
    // Distance to line is now the length of the relative point
    // vector minus the length of its projection onto the line
    // (which is zero if the projection falls outside the range
    //  of the line segment).
    var lenSq = px * px + py * py - projlenSq;
    if (lenSq < 0) {
        lenSq = 0;
    }
    return Math.sqrt(lenSq)<coronaWidth;
};

Answer 18

C#

Adapted from @Grumdrig

public static double MinimumDistanceToLineSegment(this Point p,
    Line line)
{
    var v = line.StartPoint;
    var w = line.EndPoint;

    double lengthSquared = DistanceSquared(v, w);

    if (lengthSquared == 0.0)
        return Distance(p, v);

    double t = Math.Max(0, Math.Min(1, DotProduct(p - v, w - v) / lengthSquared));
    var projection = v + t * (w - v);

    return Distance(p, projection);
}

public static double Distance(Point a, Point b)
{
    return Math.Sqrt(DistanceSquared(a, b));
}

public static double DistanceSquared(Point a, Point b)
{
    var d = a - b;
    return DotProduct(d, d);
}

public static double DotProduct(Point a, Point b)
{
    return (a.X * b.X) + (a.Y * b.Y);
}

Answer 19

Matlab code, with built-in "self test" if they call the function with no arguments:

function r = distPointToLineSegment( xy0, xy1, xyP )
% r = distPointToLineSegment( xy0, xy1, xyP )

if( nargin < 3 )
    selfTest();
    r=0;
else
    vx = xy0(1)-xyP(1);
    vy = xy0(2)-xyP(2);
    ux = xy1(1)-xy0(1);
    uy = xy1(2)-xy0(2);
    lenSqr= (ux*ux+uy*uy);
    detP= -vx*ux + -vy*uy;

    if( detP < 0 )
        r = norm(xy0-xyP,2);
    elseif( detP > lenSqr )
        r = norm(xy1-xyP,2);
    else
        r = abs(ux*vy-uy*vx)/sqrt(lenSqr);
    end
end


    function selfTest()
        %#ok<*NASGU>
        disp(['invalid args, distPointToLineSegment running (recursive)  self-test...']);

        ptA = [1;1]; ptB = [-1;-1];
        ptC = [1/2;1/2];  % on the line
        ptD = [-2;-1.5];  % too far from line segment
        ptE = [1/2;0];    % should be same as perpendicular distance to line
        ptF = [1.5;1.5];      % along the A-B but outside of the segment

        distCtoAB = distPointToLineSegment(ptA,ptB,ptC)
        distDtoAB = distPointToLineSegment(ptA,ptB,ptD)
        distEtoAB = distPointToLineSegment(ptA,ptB,ptE)
        distFtoAB = distPointToLineSegment(ptA,ptB,ptF)
        figure(1); clf;
        circle = @(x, y, r, c) rectangle('Position', [x-r, y-r, 2*r, 2*r], ...
            'Curvature', [1 1], 'EdgeColor', c);
        plot([ptA(1) ptB(1)],[ptA(2) ptB(2)],'r-x'); hold on;
        plot(ptC(1),ptC(2),'b+'); circle(ptC(1),ptC(2), 0.5e-1, 'b');
        plot(ptD(1),ptD(2),'g+'); circle(ptD(1),ptD(2), distDtoAB, 'g');
        plot(ptE(1),ptE(2),'k+'); circle(ptE(1),ptE(2), distEtoAB, 'k');
        plot(ptF(1),ptF(2),'m+'); circle(ptF(1),ptF(2), distFtoAB, 'm');
        hold off;
        axis([-3 3 -3 3]); axis equal;
    end

end

Answer 20

coded in t-sql

the point is (@px, @py) and the line segment runs from (@ax, @ay) to (@bx, @by)

create function fn_sqr (@NumberToSquare decimal(18,10)) 
returns decimal(18,10)
as 
begin
    declare @Result decimal(18,10)
    set @Result = @NumberToSquare * @NumberToSquare
    return @Result
end
go

create function fn_Distance(@ax decimal (18,10) , @ay decimal (18,10), @bx decimal(18,10),  @by decimal(18,10)) 
returns decimal(18,10)
as
begin
    declare @Result decimal(18,10)
    set @Result = (select dbo.fn_sqr(@ax - @bx) + dbo.fn_sqr(@ay - @by) )
    return @Result
end
go

create function fn_DistanceToSegmentSquared(@px decimal(18,10), @py decimal(18,10), @ax decimal(18,10), @ay decimal(18,10), @bx decimal(18,10), @by decimal(18,10)) 
returns decimal(18,10)
as 
begin
    declare @l2 decimal(18,10)
    set @l2 = (select dbo.fn_Distance(@ax, @ay, @bx, @by))
    if @l2 = 0
        return dbo.fn_Distance(@px, @py, @ax, @ay)
    declare @t decimal(18,10)
    set @t = ((@px - @ax) * (@bx - @ax) + (@py - @ay) * (@by - @ay)) / @l2
    if (@t < 0) 
        return dbo.fn_Distance(@px, @py, @ax, @ay);
    if (@t > 1) 
        return dbo.fn_Distance(@px, @py, @bx, @by);
    return dbo.fn_Distance(@px, @py,  @ax + @t * (@bx - @ax),  @ay + @t * (@by - @ay))
end
go

create function fn_DistanceToSegment(@px decimal(18,10), @py decimal(18,10), @ax decimal(18,10), @ay decimal(18,10), @bx decimal(18,10), @by decimal(18,10)) 
returns decimal(18,10)
as 
begin
    return sqrt(dbo.fn_DistanceToSegmentSquared(@px, @py , @ax , @ay , @bx , @by ))
end
go

--example execution for distance from a point at (6,1) to line segment that runs from (4,2) to (2,1)
select dbo.fn_DistanceToSegment(6, 1, 4, 2, 2, 1) 
--result = 2.2360679775

--example execution for distance from a point at (-3,-2) to line segment that runs from (0,-2) to (-2,1)
select dbo.fn_DistanceToSegment(-3, -2, 0, -2, -2, 1) 
--result = 2.4961508830

--example execution for distance from a point at (0,-2) to line segment that runs from (0,-2) to (-2,1)
select dbo.fn_DistanceToSegment(0,-2, 0, -2, -2, 1) 
--result = 0.0000000000

Answer 21

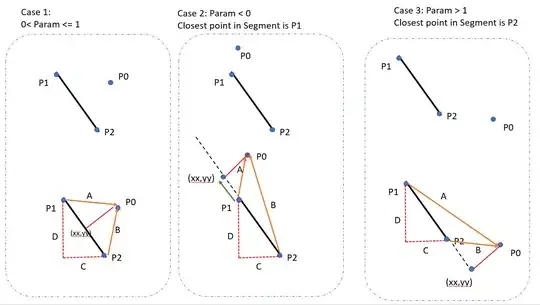
Looks like just about everyone else on StackOverflow has contributed an answer (23 answers so far), so here's my contribution for C#. This is mostly based on the answer by M. Katz, which in turn is based on the answer by Grumdrig.

   public struct MyVector
   {
      private readonly double _x, _y;


      // Constructor
      public MyVector(double x, double y)
      {
         _x = x;
         _y = y;
      }


      // Distance from this point to another point, squared
      private double DistanceSquared(MyVector otherPoint)
      {
         double dx = otherPoint._x - this._x;
         double dy = otherPoint._y - this._y;
         return dx * dx + dy * dy;
      }


      // Find the distance from this point to a line segment (which is not the same as from this 
      //  point to anywhere on an infinite line). Also returns the closest point.
      public double DistanceToLineSegment(MyVector lineSegmentPoint1, MyVector lineSegmentPoint2,
                                          out MyVector closestPoint)
      {
         return Math.Sqrt(DistanceToLineSegmentSquared(lineSegmentPoint1, lineSegmentPoint2, 
                          out closestPoint));
      }


      // Same as above, but avoid using Sqrt(), saves a new nanoseconds in cases where you only want 
      //  to compare several distances to find the smallest or largest, but don't need the distance
      public double DistanceToLineSegmentSquared(MyVector lineSegmentPoint1, 
                                              MyVector lineSegmentPoint2, out MyVector closestPoint)
      {
         // Compute length of line segment (squared) and handle special case of coincident points
         double segmentLengthSquared = lineSegmentPoint1.DistanceSquared(lineSegmentPoint2);
         if (segmentLengthSquared < 1E-7f)  // Arbitrary "close enough for government work" value
         {
            closestPoint = lineSegmentPoint1;
            return this.DistanceSquared(closestPoint);
         }

         // Use the magic formula to compute the "projection" of this point on the infinite line
         MyVector lineSegment = lineSegmentPoint2 - lineSegmentPoint1;
         double t = (this - lineSegmentPoint1).DotProduct(lineSegment) / segmentLengthSquared;

         // Handle the two cases where the projection is not on the line segment, and the case where 
         //  the projection is on the segment
         if (t <= 0)
            closestPoint = lineSegmentPoint1;
         else if (t >= 1)
            closestPoint = lineSegmentPoint2;
         else 
            closestPoint = lineSegmentPoint1 + (lineSegment * t);
         return this.DistanceSquared(closestPoint);
      }


      public double DotProduct(MyVector otherVector)
      {
         return this._x * otherVector._x + this._y * otherVector._y;
      }

      public static MyVector operator +(MyVector leftVector, MyVector rightVector)
      {
         return new MyVector(leftVector._x + rightVector._x, leftVector._y + rightVector._y);
      }

      public static MyVector operator -(MyVector leftVector, MyVector rightVector)
      {
         return new MyVector(leftVector._x - rightVector._x, leftVector._y - rightVector._y);
      }

      public static MyVector operator *(MyVector aVector, double aScalar)
      {
         return new MyVector(aVector._x * aScalar, aVector._y * aScalar);
      }

      // Added using ReSharper due to CodeAnalysis nagging

      public bool Equals(MyVector other)
      {
         return _x.Equals(other._x) && _y.Equals(other._y);
      }

      public override bool Equals(object obj)
      {
         if (ReferenceEquals(null, obj)) return false;
         return obj is MyVector && Equals((MyVector) obj);
      }

      public override int GetHashCode()
      {
         unchecked
         {
            return (_x.GetHashCode()*397) ^ _y.GetHashCode();
         }
      }

      public static bool operator ==(MyVector left, MyVector right)
      {
         return left.Equals(right);
      }

      public static bool operator !=(MyVector left, MyVector right)
      {
         return !left.Equals(right);
      }
   }

And here's a little test program.

   public static class JustTesting
   {
      public static void Main()
      {
         Stopwatch stopwatch = new Stopwatch();
         stopwatch.Start();

         for (int i = 0; i < 10000000; i++)
         {
            TestIt(1, 0, 0, 0, 1, 1, 0.70710678118654757);
            TestIt(5, 4, 0, 0, 20, 10, 1.3416407864998738);
            TestIt(30, 15, 0, 0, 20, 10, 11.180339887498949);
            TestIt(-30, 15, 0, 0, 20, 10, 33.541019662496844);
            TestIt(5, 1, 0, 0, 10, 0, 1.0);
            TestIt(1, 5, 0, 0, 0, 10, 1.0);
         }

         stopwatch.Stop();
         TimeSpan timeSpan = stopwatch.Elapsed;
      }


      private static void TestIt(float aPointX, float aPointY, 
                                 float lineSegmentPoint1X, float lineSegmentPoint1Y, 
                                 float lineSegmentPoint2X, float lineSegmentPoint2Y, 
                                 double expectedAnswer)
      {
         // Katz
         double d1 = DistanceFromPointToLineSegment(new MyVector(aPointX, aPointY), 
                                              new MyVector(lineSegmentPoint1X, lineSegmentPoint1Y), 
                                              new MyVector(lineSegmentPoint2X, lineSegmentPoint2Y));
         Debug.Assert(d1 == expectedAnswer);

         /*
         // Katz using squared distance
         double d2 = DistanceFromPointToLineSegmentSquared(new MyVector(aPointX, aPointY), 
                                              new MyVector(lineSegmentPoint1X, lineSegmentPoint1Y), 
                                              new MyVector(lineSegmentPoint2X, lineSegmentPoint2Y));
         Debug.Assert(Math.Abs(d2 - expectedAnswer * expectedAnswer) < 1E-7f);
          */

         /*
         // Matti (optimized)
         double d3 = FloatVector.DistanceToLineSegment(new PointF(aPointX, aPointY), 
                                                new PointF(lineSegmentPoint1X, lineSegmentPoint1Y), 
                                                new PointF(lineSegmentPoint2X, lineSegmentPoint2Y));
         Debug.Assert(Math.Abs(d3 - expectedAnswer) < 1E-7f);
          */
      }

      private static double DistanceFromPointToLineSegment(MyVector aPoint, 
                                             MyVector lineSegmentPoint1, MyVector lineSegmentPoint2)
      {
         MyVector closestPoint;  // Not used
         return aPoint.DistanceToLineSegment(lineSegmentPoint1, lineSegmentPoint2, 
                                             out closestPoint);
      }

      private static double DistanceFromPointToLineSegmentSquared(MyVector aPoint, 
                                             MyVector lineSegmentPoint1, MyVector lineSegmentPoint2)
      {
         MyVector closestPoint;  // Not used
         return aPoint.DistanceToLineSegmentSquared(lineSegmentPoint1, lineSegmentPoint2, 
                                                    out closestPoint);
      }
   }

As you can see, I tried to measure the difference between using the version that avoids the Sqrt() method and the normal version. My tests indicate you can maybe save about 2.5%, but I'm not even sure of that - the variations within the various test runs were of the same order of magnitude. I also tried measuring the version posted by Matti (plus an obvious optimization), and that version seems to be about 4% slower than the version based on Katz/Grumdrig code.

Edit: Incidentally, I've also tried measuring a method that finds the distance to an infinite line (not a line segment) using a cross product (and a Sqrt()), and it's about 32% faster.

Answer 22

Here is devnullicus's C++ version converted to C#. For my implementation I needed to know the point of intersection and found his solution to work well.

public static bool PointSegmentDistanceSquared(PointF point, PointF lineStart, PointF lineEnd, out double distance, out PointF intersectPoint)
{
    const double kMinSegmentLenSquared = 0.00000001; // adjust to suit.  If you use float, you'll probably want something like 0.000001f
    const double kEpsilon = 1.0E-14; // adjust to suit.  If you use floats, you'll probably want something like 1E-7f
    double dX = lineEnd.X - lineStart.X;
    double dY = lineEnd.Y - lineStart.Y;
    double dp1X = point.X - lineStart.X;
    double dp1Y = point.Y - lineStart.Y;
    double segLenSquared = (dX * dX) + (dY * dY);
    double t = 0.0;

    if (segLenSquared >= -kMinSegmentLenSquared && segLenSquared <= kMinSegmentLenSquared)
    {
        // segment is a point.
        intersectPoint = lineStart;
        t = 0.0;
        distance = ((dp1X * dp1X) + (dp1Y * dp1Y));
    }
    else
    {
        // Project a line from p to the segment [p1,p2].  By considering the line
        // extending the segment, parameterized as p1 + (t * (p2 - p1)),
        // we find projection of point p onto the line. 
        // It falls where t = [(p - p1) . (p2 - p1)] / |p2 - p1|^2
        t = ((dp1X * dX) + (dp1Y * dY)) / segLenSquared;
        if (t < kEpsilon)
        {
            // intersects at or to the "left" of first segment vertex (lineStart.X, lineStart.Y).  If t is approximately 0.0, then
            // intersection is at p1.  If t is less than that, then there is no intersection (i.e. p is not within
            // the 'bounds' of the segment)
            if (t > -kEpsilon)
            {
                // intersects at 1st segment vertex
                t = 0.0;
            }
            // set our 'intersection' point to p1.
            intersectPoint = lineStart;
            // Note: If you wanted the ACTUAL intersection point of where the projected lines would intersect if
            // we were doing PointLineDistanceSquared, then intersectPoint.X would be (lineStart.X + (t * dx)) and intersectPoint.Y would be (lineStart.Y + (t * dy)).
        }
        else if (t > (1.0 - kEpsilon))
        {
            // intersects at or to the "right" of second segment vertex (lineEnd.X, lineEnd.Y).  If t is approximately 1.0, then
            // intersection is at p2.  If t is greater than that, then there is no intersection (i.e. p is not within
            // the 'bounds' of the segment)
            if (t < (1.0 + kEpsilon))
            {
                // intersects at 2nd segment vertex
                t = 1.0;
            }
            // set our 'intersection' point to p2.
            intersectPoint = lineEnd;
            // Note: If you wanted the ACTUAL intersection point of where the projected lines would intersect if
            // we were doing PointLineDistanceSquared, then intersectPoint.X would be (lineStart.X + (t * dx)) and intersectPoint.Y would be (lineStart.Y + (t * dy)).
        }
        else
        {
            // The projection of the point to the point on the segment that is perpendicular succeeded and the point
            // is 'within' the bounds of the segment.  Set the intersection point as that projected point.
            intersectPoint = new PointF((float)(lineStart.X + (t * dX)), (float)(lineStart.Y + (t * dY)));
        }
        // return the squared distance from p to the intersection point.  Note that we return the squared distance
        // as an optimization because many times you just need to compare relative distances and the squared values
        // works fine for that.  If you want the ACTUAL distance, just take the square root of this value.
        double dpqX = point.X - intersectPoint.X;
        double dpqY = point.Y - intersectPoint.Y;

        distance = ((dpqX * dpqX) + (dpqY * dpqY));
    }

    return true;
}

Answer 23

A 2D and 3D solution

Consider a change of basis such that the line segment becomes (0, 0, 0)-(d, 0, 0) and the point (u, v, 0). The shortest distance occurs in that plane and is given by

    u ≤ 0 -> d(A, C)
0 ≤ u ≤ d -> |v|
d ≤ u     -> d(B, C)

(the distance to one of the endpoints or to the supporting line, depending on the projection to the line. The iso-distance locus is made of two half-circles and two line segments.)

In the above expression, d is the length of the segment AB, and u, v are respectivey the scalar product and (modulus of the) cross product of AB/d (unit vector in the direction of AB) and AC. Hence vectorially,

AB.AC ≤ 0             -> |AC|
    0 ≤ AB.AC ≤ AB²   -> |ABxAC|/|AB|
          AB² ≤ AB.AC -> |BC|

Answer 24

C# Version

public static FP DistanceToLineSegment(FPVector3 a, FPVector3 b, FPVector3 point)
{
  var d = b - a;
  var s = d.SqrMagnitude;
  var ds = d / s;
  var lambda = FPVector3.Dot(point - a, ds);
  var p = FPMath.Clamp01(lambda) * d;
  return (a + p - point).Magnitude;
}

Answer 25

see the Matlab GEOMETRY toolbox in the following website: http://people.sc.fsu.edu/~jburkardt/m_src/geometry/geometry.html

ctrl+f and type "segment" to find line segment related functions. the functions "segment_point_dist_2d.m" and "segment_point_dist_3d.m" are what you need.

The GEOMETRY codes are available in a C version and a C++ version and a FORTRAN77 version and a FORTRAN90 version and a MATLAB version.

Answer 26

AutoHotkeys version based on Joshua's Javascript:

plDist(x, y, x1, y1, x2, y2) {
    A:= x - x1
    B:= y - y1
    C:= x2 - x1
    D:= y2 - y1

    dot:= A*C + B*D
    sqLen:= C*C + D*D
    param:= dot / sqLen

    if (param < 0 || ((x1 = x2) && (y1 = y2))) {
        xx:= x1
        yy:= y1
    } else if (param > 1) {
        xx:= x2
        yy:= y2
    } else {
        xx:= x1 + param*C
        yy:= y1 + param*D
    }

    dx:= x - xx
    dy:= y - yy

    return sqrt(dx*dx + dy*dy)
}

Answer 27

the accepted answer does not work (e.g. distance between 0,0 and (-10,2,10,2) should be 2).

here's code that works:

   def dist2line2(x,y,line):
     x1,y1,x2,y2=line
     vx = x1 - x
     vy = y1 - y
     ux = x2-x1
     uy = y2-y1
     length = ux * ux + uy * uy
     det = (-vx * ux) + (-vy * uy) #//if this is < 0 or > length then its outside the line segment
     if det < 0:
       return (x1 - x)**2 + (y1 - y)**2
     if det > length:
       return (x2 - x)**2 + (y2 - y)**2
     det = ux * vy - uy * vx
     return det**2 / length
   def dist2line(x,y,line): return math.sqrt(dist2line2(x,y,line))

Answer 28

Didn't see a Java implementation here, so I translated the Javascript function from the accepted answer to Java code:

static double sqr(double x) {
    return x * x;
}
static double dist2(DoublePoint v, DoublePoint w) {
    return sqr(v.x - w.x) + sqr(v.y - w.y);
}
static double distToSegmentSquared(DoublePoint p, DoublePoint v, DoublePoint w) {
    double l2 = dist2(v, w);
    if (l2 == 0) return dist2(p, v);
    double t = ((p.x - v.x) * (w.x - v.x) + (p.y - v.y) * (w.y - v.y)) / l2;
    if (t < 0) return dist2(p, v);
    if (t > 1) return dist2(p, w);
    return dist2(p, new DoublePoint(
            v.x + t * (w.x - v.x),
            v.y + t * (w.y - v.y)
    ));
}
static double distToSegment(DoublePoint p, DoublePoint v, DoublePoint w) {
    return Math.sqrt(distToSegmentSquared(p, v, w));
}
static class DoublePoint {
    public double x;
    public double y;

    public DoublePoint(double x, double y) {
        this.x = x;
        this.y = y;
    }
}

Answer 29

WPF version:

public class LineSegment
{
    private readonly Vector _offset;
    private readonly Vector _vector;

    public LineSegment(Point start, Point end)
    {
        _offset = (Vector)start;
        _vector = (Vector)(end - _offset);
    }

    public double DistanceTo(Point pt)
    {
        var v = (Vector)pt - _offset;

        // first, find a projection point on the segment in parametric form (0..1)
        var p = (v * _vector) / _vector.LengthSquared;

        // and limit it so it lays inside the segment
        p = Math.Min(Math.Max(p, 0), 1);

        // now, find the distance from that point to our point
        return (_vector * p - v).Length;
    }
}

Answer 30

I've made an interactive Desmos graph to demonstrate how to achieve this:

https://www.desmos.com/calculator/kswrm8ddum

The red point is A, the green point is B, and the point C is blue. You can drag the points in the graph to see the values change. On the left, the value 's' is the parameter of the line segment (i.e. s = 0 means the point A, and s = 1 means the point B). The value 'd' is the distance from the third point to the line through A and B.

EDIT:

Fun little insight: the coordinate (s, d) is the coordinate of the third point C in the coordinate system where AB is the unit x-axis, and the unit y-axis is perpendicular to AB.

Answer 31

Python Numpy implementation for 2D coordinate array:

import numpy as np


def dist2d(p1, p2, coords):
    ''' Distance from points to a finite line btwn p1 -> p2 '''
    assert coords.ndim == 2 and coords.shape[1] == 2, 'coords is not 2 dim'
    dp = p2 - p1
    st = dp[0]**2 + dp[1]**2
    u = ((coords[:, 0] - p1[0]) * dp[0] + (coords[:, 1] - p1[1]) * dp[1]) / st

    u[u > 1.] = 1.
    u[u < 0.] = 0.

    dx = (p1[0] + u * dp[0]) - coords[:, 0]
    dy = (p1[1] + u * dp[1]) - coords[:, 1]

    return np.sqrt(dx**2 + dy**2)


# Usage:
p1 = np.array([0., 0.])
p2 = np.array([0., 10.])

# List of coordinates
coords = np.array(
    [[0., 0.],
     [5., 5.],
     [10., 10.],
     [20., 20.]
     ])

d = dist2d(p1, p2, coords)

# Single coordinate
coord = np.array([25., 25.])
d = dist2d(p1, p2, coord[np.newaxis, :])

Answer 32

Here is same thing as the C++ answer but ported to pascal. The order of the point parameter has changed to suit my code but is the same thing.

function Dot(const p1, p2: PointF): double;
begin
  Result := p1.x * p2.x + p1.y * p2.y;
end;
function SubPoint(const p1, p2: PointF): PointF;
begin
  result.x := p1.x - p2.x;
  result.y := p1.y - p2.y;
end;

function ShortestDistance2(const p,v,w : PointF) : double;
var
  l2,t : double;
  projection,tt: PointF;
begin
  // Return minimum distance between line segment vw and point p
  //l2 := length_squared(v, w);  // i.e. |w-v|^2 -  avoid a sqrt
  l2 := Distance(v,w);
  l2 := MPower(l2,2);
  if (l2 = 0.0) then begin
    result:= Distance(p, v);   // v == w case
    exit;
  end;
  // Consider the line extending the segment, parameterized as v + t (w - v).
  // We find projection of point p onto the line.
  // It falls where t = [(p-v) . (w-v)] / |w-v|^2
  t := Dot(SubPoint(p,v),SubPoint(w,v)) / l2;
  if (t < 0.0) then begin
    result := Distance(p, v);       // Beyond the 'v' end of the segment
    exit;
  end
  else if (t > 1.0) then begin
    result := Distance(p, w);  // Beyond the 'w' end of the segment
    exit;
  end;
  //projection := v + t * (w - v);  // Projection falls on the segment
  tt.x := v.x + t * (w.x - v.x);
  tt.y := v.y + t * (w.y - v.y);
  result := Distance(p, tt);
end;

Answer 33

%Matlab solution by Tim from Cody
function ans=distP2S(x0,y0,x1,y1,x2,y2)
% Point is x0,y0
z=complex(x0-x1,y0-y1);
complex(x2-x1,y2-y1);
abs(z-ans*min(1,max(0,real(z/ans))));

Answer 34

This algorithm is based on finding the intersection between the specified line and the orthogonal line, which contains the specified point, and calculating its distance. In case of a line segment, we must check if the intersection is between points of the line segment, if that's not the case then the minimum distance is between the specified point and one of the ending points of the line segment. This is a C# implementation.

Double Distance(Point a, Point b)
{
    double xdiff = a.X - b.X, ydiff = a.Y - b.Y;
    return Math.Sqrt((long)xdiff * xdiff + (long)ydiff * ydiff);
}

Boolean IsBetween(double x, double a, double b)
{
    return ((a <= b && x >= a && x <= b) || (a > b && x <= a && x >= b));
}

Double GetDistance(Point pt, Point pt1, Point pt2, out Point intersection)
{
    Double a, x, y, R;

    if (pt1.X != pt2.X) {
        a = (double)(pt2.Y - pt1.Y) / (pt2.X - pt1.X);
        x = (a * (pt.Y - pt1.Y) + a * a * pt1.X + pt.X) / (a * a + 1);
        y = a * x + pt1.Y - a * pt1.X; }
    else { x = pt1.X;  y = pt.Y; }

    if (IsBetween(x, pt1.X, pt2.X) && IsBetween(y, pt1.Y, pt2.Y)) {
        intersection = new Point((int)x, (int)y);
        R = Distance(intersection, pt); }
    else {
        double d1 = Distance(pt, pt1), d2 = Distance(pt, pt2);
        if (d1 < d2) { intersection = pt1; R = d1; }
        else { intersection = pt2; R = d2; }}

    return R;
}

Answer 35

GLSL version:

// line (a -> b ) point p[enter image description here][1]
float distanceToLine(vec2 a, vec2 b, vec2 p) {
    float aside = dot((p - a),(b - a));
    if(aside< 0.0) return length(p-a);
    float bside = dot((p - b),(a - b));
    if(bside< 0.0) return length(p-b);
    vec2 pointOnLine = (bside*a + aside*b)/pow(length(a-b),2.0);
    return length(p - pointOnLine);
}

Answer 36

Here is one based on vector math; this solution will also work for higher dimensions and also report on the interection point (on the line segment).

def dist(x1,y1,x2,y2,px,py):
    a = np.array([[x1,y1]]).T
    b = np.array([[x2,y2]]).T
    x = np.array([[px,py]]).T
    tp = (np.dot(x.T, b) - np.dot(a.T, b)) / np.dot(b.T, b)
    tp = tp[0][0]
    tmp = x - (a + tp*b)
    d = np.sqrt(np.dot(tmp.T,tmp)[0][0])
    return d, a+tp*b

x1,y1=2.,2.
x2,y2=5.,5.
px,py=4.,1.

d, inters = dist(x1,y1, x2,y2, px,py)
print (d)
print (inters)

Result is

2.1213203435596424
[[2.5]
 [2.5]]

The math is explained here

https://brilliant.org/wiki/distance-between-point-and-line/

Answer 37

Solution for dart and flutter:

import 'dart:math' as math;
 class Utils {
   static double shortestDistance(Point p1, Point p2, Point p3){
      double px = p2.x - p1.x;
      double py = p2.y - p1.y;
      double temp = (px*px) + (py*py);
      double u = ((p3.x - p1.x)*px + (p3.y - p1.y)* py) /temp;
      if(u>1){
        u=1;
      }
      else if(u<0){
        u=0;
      }
      double x = p1.x + u*px;
      double y = p1.y + u*py;
      double dx = x - p3.x;
      double dy = y - p3.y;
      double dist = math.sqrt(dx*dx+dy*dy);
      return dist;
   }
}

class Point {
  double x;
  double y;
  Point(this.x, this.y);
}

Answer 38

The above function is not working on vertical lines. Here is a function that is working fine! Line with points p1, p2. and CheckPoint is p;

public float DistanceOfPointToLine2(PointF p1, PointF p2, PointF p)
{
  //          (y1-y2)x + (x2-x1)y + (x1y2-x2y1)
  //d(P,L) = --------------------------------
  //         sqrt( (x2-x1)pow2 + (y2-y1)pow2 )

  double ch = (p1.Y - p2.Y) * p.X + (p2.X - p1.X) * p.Y + (p1.X * p2.Y - p2.X * p1.Y);
  double del = Math.Sqrt(Math.Pow(p2.X - p1.X, 2) + Math.Pow(p2.Y - p1.Y, 2));
  double d = ch / del;
  return (float)d;
}

Answer 39

Here's the code I ended up writing. This code assumes that a point is defined in the form of {x:5, y:7}. Note that this is not the absolute most efficient way, but it's the simplest and easiest-to-understand code that I could come up with.

// a, b, and c in the code below are all points

function distance(a, b)
{
    var dx = a.x - b.x;
    var dy = a.y - b.y;
    return Math.sqrt(dx*dx + dy*dy);
}

function Segment(a, b)
{
    var ab = {
        x: b.x - a.x,
        y: b.y - a.y
    };
    var length = distance(a, b);

    function cross(c) {
        return ab.x * (c.y-a.y) - ab.y * (c.x-a.x);
    };

    this.distanceFrom = function(c) {
        return Math.min(distance(a,c),
                        distance(b,c),
                        Math.abs(cross(c) / length));
    };
}

Answer 40

Matlab direct Grumdrig implementation

function ans=distP2S(px,py,vx,vy,wx,wy)
% [px py vx vy wx wy]
  t=( (px-vx)*(wx-vx)+(py-vy)*(wy-vy) )/idist(vx,wx,vy,wy)^2;
  [idist(px,vx,py,vy) idist(px,vx+t*(wx-vx),py,vy+t*(wy-vy)) idist(px,wx,py,wy) ];
  ans(1+(t>0)+(t>1)); % <0 0<=t<=1 t>1     
 end

function d=idist(a,b,c,d)
 d=abs(a-b+1i*(c-d));
end

Answer 41

If its an infinite line, not a line segment, the simplest way is this (in ruby), where mx + b is the line and (x1, y1) is the known point

(y1 - mx1 - b).abs / Math.sqrt(m**2 + 1)

Answer 42

Just came across this and thought I'd add a Lua implementation. It assumes that points are given as tables {x=xVal, y=yVal} and the line or segment is given by a table containing two points (see example below):

function distance( P1, P2 )
    return math.sqrt((P1.x-P2.x)^2 + (P1.y-P2.y)^2)
end

-- Returns false if the point lies beyond the reaches of the segment
function distPointToSegment( line, P )
    if line[1].x == line[2].x and line[1].y == line[2].y then
        print("Error: Not a line!")
        return false
    end

    local d = distance( line[1], line[2] )

    local t = ((P.x - line[1].x)*(line[2].x - line[1].x) + (P.y - line[1].y)*(line[2].y - line[1].y))/(d^2)

    local projection = {}
    projection.x = line[1].x + t*(line[2].x-line[1].x)
    projection.y = line[1].y + t*(line[2].y-line[1].y)

    if t >= 0 and t <= 1 then   -- within line segment?
        return distance( projection, {x=P.x, y=P.y} )
    else
        return false
    end
end

-- Returns value even if point is further down the line (outside segment)
function distPointToLine( line, P )
    if line[1].x == line[2].x and line[1].y == line[2].y then
        print("Error: Not a line!")
        return false
    end

    local d = distance( line[1], line[2] )

    local t = ((P.x - line[1].x)*(line[2].x - line[1].x) + (P.y - line[1].y)*(line[2].y - line[1].y))/(d^2)

    local projection = {}
    projection.x = line[1].x + t*(line[2].x-line[1].x)
    projection.y = line[1].y + t*(line[2].y-line[1].y)

    return distance( projection, {x=P.x, y=P.y} )
end

Example usage:

local P1 = {x = 0, y = 0}
local P2 = {x = 10, y = 10}
local line = { P1, P2 }
local P3 = {x = 7, y = 15}
print(distPointToLine( line, P3 ))  -- prints 5.6568542494924
print(distPointToSegment( line, P3 )) -- prints false

Answer 43

A little cleaner solution in JavaScript based on this formula:

distToSegment: function (point, linePointA, linePointB){

    var x0 = point.X;
    var y0 = point.Y;

    var x1 = linePointA.X;
    var y1 = linePointA.Y;

    var x2 = linePointB.X;
    var y2 = linePointB.Y;

    var Dx = (x2 - x1);
    var Dy = (y2 - y1);

    var numerator = Math.abs(Dy*x0 - Dx*y0 - x1*y2 + x2*y1);
    var denominator = Math.sqrt(Dx*Dx + Dy*Dy);
    if (denominator == 0) {
        return this.dist2(point, linePointA);
    }

    return numerator/denominator;

}

Answer 44

Wanted to do this in GLSL, but it's better to avoid all those conditionals if possible. Using clamp() avoids the two end-point cases:

// find closest point to P on line segment AB:
vec3 closest_point_on_line_segment(in vec3 P, in vec3 A, in vec3 B) {
    vec3 AP = P - A, AB = B - A;
    float l = dot(AB, AB);
    if (l <= 0.0000001) return A;    // A and B are practically the same
    return AP - AB*clamp(dot(AP, AB)/l, 0.0, 1.0);  // do the projection
}

If you can be sure that A and B are never very close to each other, this can be simplified to remove the if(). In fact, even if A and B are the same, my GPU still gives the right result with this condition-free version (but this is using pre-OpenGL 4.1 in which GLSL divide by zero is undefined):

// find closest point to P on line segment AB:
vec3 closest_point_on_line_segment(in vec3 P, in vec3 A, in vec3 B) {
    vec3 AP = P - A, AB = B - A;
    return AP - AB*clamp(dot(AP, AB)/dot(AB, AB), 0.0, 1.0);
}

To compute the distance is trivial -- GLSL provides a distance() function which you can use on this closest point and P.

Inspired by Iñigo Quilez's code for a capsule distance function

Answer 45

Same as this answer, except in Visual Basic. Makes it usable as a User Defined Function in Microsoft Excel and VBA/macros.

The function returns the closest distance from point (x,y) to the segment defined by (x1,y1) and (x2,y2)

Function DistanceToSegment(x As Double, y As Double, x1 As Double, y1 As Double, x2 As Double, y2 As Double)

  Dim A As Double
  A = x - x1
  Dim B As Double
  B = y - y1
  Dim C  As Double
  C = x2 - x1
  Dim D As Double
  D = y2 - y1

  Dim dot As Double
  dot = A * C + B * D
  Dim len_sq As Double
  len_sq = C * C + D * D
  Dim param As Double
  param = -1

  If (len_sq <> 0) Then
      param = dot / len_sq
  End If

  Dim xx As Double
  Dim yy As Double

  If (param < 0) Then
    xx = x1
    yy = y1
  ElseIf (param > 1) Then
    xx = x2
    yy = y2
  Else
    xx = x1 + param * C
    yy = y1 + param * D
  End If

  Dim dx As Double
  dx = x - xx
  Dim dy As Double
  dy = y - yy

  DistanceToSegment = Math.Sqr(dx * dx + dy * dy)

End Function

Answer 46

Lua: Finds minimum distance between a line segment(not the whole line) and a point

function solveLinearEquation(A1,B1,C1,A2,B2,C2)
--it is the implitaion of a method of solving linear equations in x and y
  local f1 = B1*C2 -B2*C1
  local f2 = A2*C1-A1*C2
  local f3 = A1*B2 -A2*B1
  return {x= f1/f3, y= f2/f3}
end


function pointLiesOnLine(x,y,x1,y1,x2,y2)
  local dx1 = x-x1
  local  dy1 = y-y1
  local dx2 = x-x2
  local  dy2 = y-y2
  local crossProduct = dy1*dx2 -dx1*dy2

if crossProduct ~= 0  then  return  false
else
  if ((x1>=x) and (x>=x2)) or ((x2>=x) and (x>=x1)) then
    if ((y1>=y) and (y>=y2)) or ((y2>=y) and (y>=y1)) then
      return true
    else return false end
  else  return false end
end
end


function dist(x1,y1,x2,y2)
  local dx = x1-x2
  local dy = y1-y2
  return math.sqrt(dx*dx + dy* dy)
 end


function findMinDistBetnPointAndLine(x1,y1,x2,y2,x3,y3)
-- finds the min  distance between (x3,y3) and line (x1,y2)--(x2,y2)
   local A2,B2,C2,A1,B1,C1
   local dx = y2-y1
   local dy = x2-x1
   if dx == 0 then A2=1 B2=0 C2=-x3 A1=0 B1=1 C1=-y1 
   elseif dy == 0 then A2=0 B2=1 C2=-y3 A1=1 B1=0 C1=-x1
   else
      local m1 = dy/dx
      local m2 = -1/m1
      A2=m2 B2=-1 C2=y3-m2*x3 A1=m1 B1=-1 C1=y1-m1*x1
   end
 local intsecPoint= solveLinearEquation(A1,B1,C1,A2,B2,C2)
if pointLiesOnLine(intsecPoint.x, intsecPoint.y,x1,y1,x2,y2) then
   return dist(intsecPoint.x, intsecPoint.y, x3,y3)
 else
   return math.min(dist(x3,y3,x1,y1),dist(x3,y3,x2,y2))
end
end

Answer 47

This answer is based on the accepted answer's JavaScript solution. It's mainly just formatted nicer, with longer function names, and of course shorter function syntax because it's in ES6 + CoffeeScript.

JavaScript version (ES6)

distanceSquared = (v, w)=> Math.pow(v.x - w.x, 2) + Math.pow(v.y - w.y, 2);
distance = (v, w)=> Math.sqrt(distanceSquared(v, w));

distanceToLineSegmentSquared = (p, v, w)=> {
    l2 = distanceSquared(v, w);
    if (l2 === 0) {
        return distanceSquared(p, v);
    }
    t = ((p.x - v.x) * (w.x - v.x) + (p.y - v.y) * (w.y - v.y)) / l2;
    t = Math.max(0, Math.min(1, t));
    return distanceSquared(p, {
        x: v.x + t * (w.x - v.x),
        y: v.y + t * (w.y - v.y)
    });
}
distanceToLineSegment = (p, v, w)=> {
    return Math.sqrt(distanceToLineSegmentSquared(p, v));
}

CoffeeScript version

distanceSquared = (v, w)-> (v.x - w.x) ** 2 + (v.y - w.y) ** 2
distance = (v, w)-> Math.sqrt(distanceSquared(v, w))

distanceToLineSegmentSquared = (p, v, w)->
    l2 = distanceSquared(v, w)
    return distanceSquared(p, v) if l2 is 0
    t = ((p.x - v.x) * (w.x - v.x) + (p.y - v.y) * (w.y - v.y)) / l2
    t = Math.max(0, Math.min(1, t))
    distanceSquared(p, {
        x: v.x + t * (w.x - v.x)
        y: v.y + t * (w.y - v.y)
    })

distanceToLineSegment = (p, v, w)->
    Math.sqrt(distanceToLineSegmentSquared(p, v, w))

Answer 48

in R

     #distance beetween segment ab and point c in 2D space
getDistance_ort_2 <- function(a, b, c){
  #go to complex numbers
  A<-c(a[1]+1i*a[2],b[1]+1i*b[2])
  q=c[1]+1i*c[2]
  
  #function to get coefficients of line (ab)
  getAlphaBeta <- function(A)
  { a<-Re(A[2])-Re(A[1])
    b<-Im(A[2])-Im(A[1])
    ab<-as.numeric()
    ab[1] <- -Re(A[1])*b/a+Im(A[1])
    ab[2] <-b/a
    if(Im(A[1])==Im(A[2])) ab<- c(Im(A[1]),0)
    if(Re(A[1])==Re(A[2])) ab <- NA
    return(ab)
  }
  
  #function to get coefficients of line ortogonal to line (ab) which goes through point q
  getAlphaBeta_ort<-function(A,q)
  { ab <- getAlphaBeta(A) 
  coef<-c(Re(q)/ab[2]+Im(q),-1/ab[2])
  if(Re(A[1])==Re(A[2])) coef<-c(Im(q),0)
  return(coef)
  }
  
  #function to get coordinates of interception point 
  #between line (ab) and its ortogonal which goes through point q
  getIntersection_ort <- function(A, q){
    A.ab <- getAlphaBeta(A)
    q.ab <- getAlphaBeta_ort(A,q)
    if (!is.na(A.ab[1])&A.ab[2]==0) {
      x<-Re(q)
      y<-Im(A[1])}
    if (is.na(A.ab[1])) {
      x<-Re(A[1])
      y<-Im(q)
    } 
    if (!is.na(A.ab[1])&A.ab[2]!=0) {
      x <- (q.ab[1] - A.ab[1])/(A.ab[2] - q.ab[2])
      y <- q.ab[1] + q.ab[2]*x}
    xy <- x + 1i*y  
    return(xy)
  }
  
  intersect<-getIntersection_ort(A,q)
  if ((Mod(A[1]-intersect)+Mod(A[2]-intersect))>Mod(A[1]-A[2])) {dist<-min(Mod(A[1]-q),Mod(A[2]-q))
  } else dist<-Mod(q-intersect)
  return(dist)
}



 

Answer 49

In javascript using Geometry:

var a = { x:20, y:20};//start segment    
var b = { x:40, y:30};//end segment   
var c = { x:37, y:14};//point   

// magnitude from a to c    
var ac = Math.sqrt( Math.pow( ( a.x - c.x ), 2 ) + Math.pow( ( a.y - c.y ), 2) );    
// magnitude from b to c   
var bc = Math.sqrt( Math.pow( ( b.x - c.x ), 2 ) + Math.pow( ( b.y - c.y ), 2 ) );    
// magnitude from a to b (base)     
var ab = Math.sqrt( Math.pow( ( a.x - b.x ), 2 ) + Math.pow( ( a.y - b.y ), 2 ) );    
 // perimeter of triangle     
var p = ac + bc + ab;    
 // area of the triangle    
var area = Math.sqrt( p/2 * ( p/2 - ac) * ( p/2 - bc ) * ( p/2 - ab ) );    
 // height of the triangle = distance    
var h = ( area * 2 ) / ab;    
console.log ("height: " + h);

Answer 50

Eigen C++ Version for 3D line segment and point

// Return minimum distance between line segment: head--->tail and point
double MinimumDistance(Eigen::Vector3d head, Eigen::Vector3d tail,Eigen::Vector3d point)
{
    double l2 = std::pow((head - tail).norm(),2);
    if(l2 ==0.0) return (head - point).norm();// head == tail case

    // Consider the line extending the segment, parameterized as head + t (tail - point).
    // We find projection of point onto the line.
    // It falls where t = [(point-head) . (tail-head)] / |tail-head|^2
    // We clamp t from [0,1] to handle points outside the segment head--->tail.

    double t = max(0,min(1,(point-head).dot(tail-head)/l2));
    Eigen::Vector3d projection = head + t*(tail-head);

    return (point - projection).norm();
}

Answer 51

Here's a self contained Delphi / Pascal version of the function based on Joshua's answer up above. Uses TPoint for VCL screen graphics, but should be easy to adjust as needed.

function DistancePtToSegment( pt, pt1, pt2: TPoint): double;
var
   a, b, c, d: double;
   len_sq: double;
   param: double;
   xx, yy: double;
   dx, dy: double;
begin
   a := pt.x - pt1.x;
   b := pt.y - pt1.y;
   c := pt2.x - pt1.x;
   d := pt2.y - pt1.y;

   len_sq := (c * c) + (d * d);
   param := -1;

   if (len_sq <> 0) then
   begin
      param := ((a * c) + (b * d)) / len_sq;
   end;

   if param < 0 then
   begin
      xx := pt1.x;
      yy := pt1.y;
   end
   else if param > 1 then
   begin
      xx := pt2.x;
      yy := pt2.y;
   end
   else begin
      xx := pt1.x + param * c;
      yy := pt1.y + param * d;
   end;

   dx := pt.x - xx;
   dy := pt.y - yy;
   result := sqrt( (dx * dx) + (dy * dy))
end;

Answer 52

Swift implementation of http://paulbourke.net/geometry/pointlineplane/source.c

    static func magnitude(p1: CGPoint, p2: CGPoint) -> CGFloat {
        let vector = CGPoint(x: p2.x - p1.x, y: p2.y - p1.y)
        return sqrt(pow(vector.x, 2) + pow(vector.y, 2))
    }

    /// http://paulbourke.net/geometry/pointlineplane/
    /// http://paulbourke.net/geometry/pointlineplane/source.c
    static func pointDistanceToLine(point: CGPoint, lineStart: CGPoint, lineEnd: CGPoint) -> CGFloat? {

        let lineMag = magnitude(p1: lineEnd, p2: lineStart)
        let u = (((point.x - lineStart.x) * (lineEnd.x - lineStart.x)) +
                ((point.y - lineStart.y) * (lineEnd.y - lineStart.y))) /
                (lineMag * lineMag)

        if u < 0 || u > 1 {
            // closest point does not fall within the line segment
            return nil
        }

        let intersectionX = lineStart.x + u * (lineEnd.x - lineStart.x)
        let intersectionY = lineStart.y + u * (lineEnd.y - lineStart.y)

        return magnitude(p1: point, p2: CGPoint(x: intersectionX, y: intersectionY))
    }

Answer 53

Here is SQL implementation for HSQLDB:

CREATE FUNCTION dist_to_segment(px double, py double, vx double, vy double, wx double, wy double)
  RETURNS double
BEGIN atomic
   declare l2 double;
   declare t double;
   declare nx double;
   declare ny double;
   set l2 =(vx - wx)*(vx - wx) + (vy - wy)*(vy - wy);
   IF l2 = 0 THEN
     RETURN sqrt((vx - px)*(vx - px) + (vy - py)*(vy - py));
   ELSE
     set t = ((px - vx) * (wx - vx) + (py - vy) * (wy - vy)) / l2;
     set t = GREATEST(0, LEAST(1, t));
     set nx=vx + t * (wx - vx);
     set ny=vy + t * (wy - vy);
     RETURN sqrt((nx - px)*(nx - px) + (ny - py)*(ny - py));
   END IF;
END;

And implementation for Postgres:

CREATE FUNCTION dist_to_segment(px numeric, py numeric, vx numeric, vy numeric, wx numeric, wy numeric)
  RETURNS numeric
AS $$
   declare l2 numeric;
   declare t numeric;
   declare nx numeric;
   declare ny numeric;
BEGIN 
   l2 := (vx - wx)*(vx - wx) + (vy - wy)*(vy - wy);
   IF l2 = 0 THEN
     RETURN sqrt((vx - px)*(vx - px) + (vy - py)*(vy - py));
   ELSE
     t := ((px - vx) * (wx - vx) + (py - vy) * (wy - vy)) / l2;
     t := GREATEST(0, LEAST(1, t));
     nx := vx + t * (wx - vx);
     ny := vy + t * (wy - vy);
     RETURN sqrt((nx - px)*(nx - px) + (ny - py)*(ny - py));
   END IF;
END;
$$ LANGUAGE plpgsql;

Answer 54

The Lua solution

-- distance from point (px, py) to line segment (x1, y1, x2, y2)
function distPointToLine(px,py,x1,y1,x2,y2) -- point, start and end of the segment
    local dx,dy = x2-x1,y2-y1
    local length = math.sqrt(dx*dx+dy*dy)
    dx,dy = dx/length,dy/length -- normalization
    local p = dx*(px-x1)+dy*(py-y1)
    if p < 0 then
        dx,dy = px-x1,py-y1
        return math.sqrt(dx*dx+dy*dy), x1, y1 -- distance, nearest point
    elseif p > length then
        dx,dy = px-x2,py-y2
        return math.sqrt(dx*dx+dy*dy), x2, y2 -- distance, nearest point
    end
    return math.abs(dy*(px-x1)-dx*(py-y1)), x1+dx*p, y1+dy*p -- distance, nearest point
end

For polyline (line with more than two segments):

-- if the (poly-)line has several segments, just iterate through all of them:
function nearest_sector_in_line (x, y, line)
    local x1, y1, x2, y2, min_dist
    local ax,ay = line[1], line[2]
    for j = 3, #line-1, 2 do
        local bx,by = line[j], line[j+1]
        local dist = distPointToLine(x,y,ax,ay,bx,by)
        if not min_dist or dist < min_dist then
            min_dist = dist
            x1, y1, x2, y2 = ax,ay,bx,by
        end
        ax, ay = bx, by
    end
    return x1, y1, x2, y2
end

Example:

-- call it:
local x1, y1, x2, y2 = nearest_sector_in_line (7, 4, {0,0, 10,0, 10,10, 0,10})

Answer 55

You can try the library for PHP geo-math-php

composer require rkondratuk/geo-math-php:^1

Example:

<?php

use PhpGeoMath\Model\GeoSegment;
use PhpGeoMath\Model\Polar3dPoint;

$polarPoint1 = new Polar3dPoint(
    40.758742779050706, -73.97855507715238, Polar3dPoint::EARTH_RADIUS_IN_METERS
);

$polarPoint2 = new Polar3dPoint(
    40.74843388072615, -73.98566565776102, Polar3dPoint::EARTH_RADIUS_IN_METERS
);

$polarPoint3 = new Polar3dPoint(
    40.74919365249446, -73.98133456388013, Polar3dPoint::EARTH_RADIUS_IN_METERS
);

$arcSegment = new GeoSegment($polarPoint1, $polarPoint2);
$nearestPolarPoint = $arcSegment->calcNearestPoint($polarPoint3);

// Shortest distance from point-3 to segment(point-1, point-2)
$geoDistance = $nearestPolarPoint->calcGeoDistanceToPoint($polarPoint3);

Answer 56

I needed a Godot (GDscript) implementation of this so I wrote one based on grumdrig's accepted answer:

func minimum_distance(v: Vector2, w: Vector2, p: Vector2):
    # Return minimum distance between line segment vw and point p
    var l2: float = (v - w).length_squared()  # i.e. |w-v|^2 -  avoid a sqrt
    if l2 == 0.0:
        return p.distance_to(v) # v == w case

    # Consider the line extending the segment, parameterized as v + t (w - v).
    # We find projection of point p onto the line.
    # It falls where t = [(p-v) . (w-v)] / |w-v|^2
    # We clamp t from [0,1] to handle points outside the segment vw.
    var t: float = max(0, min(1, (p - v).dot(w - v) / l2))
    var projection: Vector2 = v + t * (w - v)  # Projection falls on the segment
    
    return p.distance_to(projection)