3

I'm creating a model to optimize purchase orders.

The amount to be ordered must be greater than 500 or equal to zero.

How do I define such a constraint in Solver?

I tried a binary constraint and I also tried several different formulas but nothing seems to work.

Basically I need to be able to express OR in Solver, how do I do that?

EDIT: in the following link you may see the excel file I'm using: Click here

Delete my account
  • 165

2 Answers2

2

So 0 is allowed, 1 is not allowed, 499 is not allowed, and 501 is allowed? Looks like a non-contiguous area. So it's not a pure optimization problem but also a kind of combinatorial problem. I'm afraid Solver can't handle this.

You should analyze two use cases separately:

  • The amount is zero (fixed value, simple calculation);
  • The amount is 500 or greater (optimize in Solver using constraint >=500);

and then compare these two cases using an IF formula.

EDIT:

I tried to use "binary" and "integer" constraints as Karl suggested but they did not work.

  • Create a binary variable 0-1 and a continuous variable >=500, and then use IF to either copy the continuous variable or write 0 to the purchases value
  • Create a binary variable 0-1 and a continuous variable >=500, and then calculate purchases as their product
  • Create an integer variable >=499, and then use IF to replace 499 by 0 for the purchases value

In all cases, the result was often wrong and depended on initial conditions. Apparently Solver doesn't like such things.

Then I thought about applying my above proposal to all six purchase values, and optimizing them independently, for example, by optimizing the sum of costs for all months. But it turns out that they are not independent: the opening inventory depends on the previous month, and the optimal purchase for a month depends on whether a purchase was made in the previous month. So it't not possible to add a simple IF to each month.

The best I could do is the following.

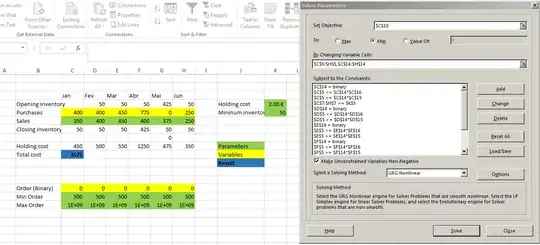
I added a binary variable 0-1 and a continuous variable >=500, and calculated each month's purchases using IF. But I optimized only the continuous variables using Solver. The binary variables are a parameter. That is, we select the months when a purchase will be made, then use the Solver to calculate the values of these purchases, and then note the resulting total cost.

This should be repeated for all combinations of purchases and non-purchases. The number of these combinations is 26=64. But actually, if you don't purchase anything in January, you end up with a negative closing inventory which is not allowed. So there are only 32 valid combinations. I added formulae to calculate the binary values from the combination index, iterated the index 32 times, launched the Solver each time by hand and copied the results "as values only" for each combination.

The result is that minimum cost is 4 625,00 € and there are two combinations to reach this value.

Here is the file uploaded to Google Docs, with a Solver screenshot.

Launching Solver multiple times by hand is tedious, I believe it can be automated using macros.

Goblin Alchemist
  • 205
1

Create a binary variable by adding a constraint stating that the value of the variable (in the objective function) is binary. The coefficient of this variable in the objective function must be 0. then you add the following constraints as you would normally do:

-500B+X>=0 (never go under 500)

-MB+X<=0 (combined with previous constraint forces 0 when B is 0)

B= Binary variable1

M=Very large positive number (Greater than X can ever be)

X= continuous variable

[Edit]

I understand you want to do something like this (I also made some changes in your sheets file, but I cant share the excel file I worked on here):

enter image description here

Karl
  • 73