-3

Why is it that Microsoft Excel 7 says that 8^(-1^(-8^7))) = 8 while Wolfram Alpha says it equals 1/8?
These results are the same if I substitute -2097152.0 for -8^7.
Now -1 to any power is -1. Therefore -1^(-8^7) = -1. And 8^-1=1/8.
Excel is wrong.
Try it and see!

Geezer
  • 15

4 Answers4

3

Excel and Wolfram Alpha have difference precedence rules for parsing an expression like this involving exponentiation and unary minus.

- x ^ y

Excel treats unary minus as higher precedence and does it first, evaluating the expression as:

( - x ) ^ y

Wolfram Alpha does the exponentiation first, evaluating the expression as:

- ( x ^ y )
Nicole Hamilton
  • 10,233
2

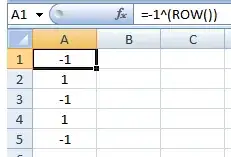
The problem is that in Excel the minus sign is used to signify both the subtraction operator and the unary sign. It is easy to illustrate this. In A1 enter:

=-1^(ROW())

and copy down:

enter image description here

The flip/flopping positive/negative indicates that Excel sees the minus sign as a unary and treats this formula like:

=(-1)^(ROW())

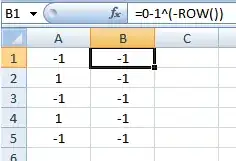
Now in B1 enter:

=0-1^(-ROW())

and copy down:

enter image description here

The lack of flip/flopping indicates that Excel sees the minus sign as a subtraction operator and treats this formula like:

=0-(1^(-ROW()))

Of course, the user can always control the precedence by using parenthesis.

EDIT#1:

See Bill Jelen's explanation

Gary's Student
  • 19,636
1

Wolfram Alpha does this:

-(1-2097152) = -(1) = -1

8-1 = 1/8

Excel, on the other hand, does this:

(-1)-2097152 = 1

81 = 8

Indeed, Excel is wrong - it should exponentiate first, then negate. Try this formula: =8^(-(1^(-8^7)))

Now -1 to any power is -1

As var firstName already pointed out, that's incorrect. However, it's true that -1N = -1 is true for any N - again, because you should exponentiate first, then negate.

Community
  • 1
gronostaj
  • 58,482
0

That's incorrect. -1^2 is 1. However, -1 to any odd power is -1; that is true. Using perfectly sensible logic, you can say that 8^(-1^(-8^7)). -8 ^ 7 = -2,097,152, an even number; therefore, -1^(-2,097,152) is 1/(-1^(2,097,152)) which reduces to 1/1 or simply 1, and 8^1 is 8. Your entry to WolframAlpha is flawed in some way.

EDIT: I did the calculation on Wolfram and it turns out that you entered it wrong. You're supposed to isolate the -1 further from the base, like this: 

8^( (-1)^(-8^7) )

Wolfram spit this out back at me (identical to my entry):

8^((-1)^(-8^7))
var firstName
  • 1,797