Introduction
This article explains how to estimate the coefficients of generating functions involving logarithms and roots.
You first may need to familiarise yourself with:
Theorems
Standard Function Scale
Theorem from Flajolet and Odlyzko[1].
If:

where  then:
then:
![{\displaystyle [z^{n}]f(z)\sim {\frac {n^{-\alpha -1}}{\Gamma (-\alpha )}}(\log n)^{\gamma }(\log \log n)^{\delta }\quad ({\text{as }}n\to \infty )}](../_assets_/eb734a37dd21ce173a46342d1cc64c92/7b39b05f6da33eecb12332a097057374f3529cd7.svg)
Singularity Analysis
Theorem from Flajolet and Sedgewick[2].
If  has a singularity at
has a singularity at  and:
and:

where  then:
then:
![{\displaystyle [z^{n}]f(z)\sim \zeta ^{-n}{\frac {n^{-\alpha -1}}{\Gamma (-\alpha )}}(\log n)^{\gamma }(\log \log n)^{\delta }\quad ({\text{as }}n\to \infty )}](../_assets_/eb734a37dd21ce173a46342d1cc64c92/6d2a6c160f6ca4d783305abb4eeca925a5f55313.svg)
The significance of the latter theorem is we only need an approximation of  .
.
Branch points
Before going into the proof, I will explain what it is about roots and logarithms that mean we have to treat them differently to meromorphic functions.
Polar coordinates
Complex numbers can be expressed in two forms: Cartesian coordinates ( ) or polar coordinates
) or polar coordinates  , where
, where  is the distance from the origin or modulus and
is the distance from the origin or modulus and  is the angle relative to the positive
is the angle relative to the positive  axis or argument.
axis or argument.
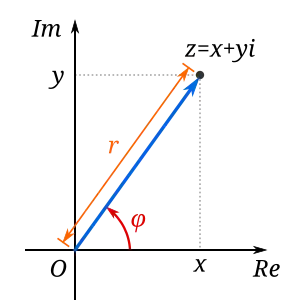
For complex functions  of complex variables
of complex variables  we can draw a 3-dimensional graph where the
we can draw a 3-dimensional graph where the  and
and  axes are the real and imaginary components respectively of the
axes are the real and imaginary components respectively of the  variable and the
variable and the  axis is either the the modulus or the argument of the function
axis is either the the modulus or the argument of the function  .
.
For roots and logarithms, if we use the argument of the function for the  axis, we see a discontinuity that restricts where we can draw the contour when we want to integrate the function.
axis, we see a discontinuity that restricts where we can draw the contour when we want to integrate the function.

The gap you can see along the negative  axis is the discontinuity.
axis is the discontinuity.
Root and logarithmic functions do not have poles about which we can do a Laurent expansion. Instead, we need to draw our contours to avoid these gaps or discontinuities. This is why in what follows we use contours with slits or wedges taken out of them.
Proof of standard function scale
Proof due to Sedgewick, Flajolet and Odlyzko[3]
The proof for the estimate of the coefficient of the first term.
By Cauchy's coefficient formula
^{\alpha }\left({\frac {1}{z}}\log {\frac {1}{1-z}}\right)^{\gamma }\left({\frac {1}{z}}\log \left({\frac {1}{z}}\log {\frac {1}{1-z}}\right)\right)^{\delta }={\frac {1}{2\pi i}}\int _{C}(1-z)^{\alpha }\left({\frac {1}{z}}\log {\frac {1}{1-z}}\right)^{\gamma }\left({\frac {1}{z}}\log \left({\frac {1}{z}}\log {\frac {1}{1-z}}\right)\right)^{\delta }{\frac {dz}{z^{n+1}}}}](../_assets_/eb734a37dd21ce173a46342d1cc64c92/ae6f06d82faaae1b5c5c921383fbad4c14e58b93.svg)
where  is a circle centred at the origin.
is a circle centred at the origin.

It is possible to deform  without changing the value of the contour integral above.
without changing the value of the contour integral above.
We will deform  by putting a slit through it along the real axis from 1 to
by putting a slit through it along the real axis from 1 to  .
.

We increase the radius of the circle to  , which reduces its contribution to the integrand to 0.
, which reduces its contribution to the integrand to 0.
Therefore, the contour integration around  above is equivalent to the contour integration around the contour which starts at
above is equivalent to the contour integration around the contour which starts at  , winds around 1 and ends at
, winds around 1 and ends at  , which we will call
, which we will call  .
.

While we don't know much about the behaviour of the integral around the contour  , we do know about a similar contour
, we do know about a similar contour  (the Hankel contour) which winds around the origin at a distance of 1.
(the Hankel contour) which winds around the origin at a distance of 1.

We can calculate the integral around  by turning it into an integral around
by turning it into an integral around  . Formally:
. Formally:
 [4]
[4]
Such that  .
.
Informally this means we want to find a function  which turns the contour
which turns the contour  into
into  . Geometrically, we move the contour to the left by 1 and multiply it by
. Geometrically, we move the contour to the left by 1 and multiply it by  :
:

But, we still want the integrand around  to be equivalent to the integrand around
to be equivalent to the integrand around  . We do this by dividing the variable by
. We do this by dividing the variable by  and adding 1:
and adding 1:

Therefore, we get the following substitution[5]:

We have:
 (as
(as  )
)
and:

Therefore,
 [6]
[6]
Putting it all together:
^{\alpha }\left({\frac {1}{z}}\log {\frac {1}{1-z}}\right)^{\gamma }\left({\frac {1}{z}}\log \left({\frac {1}{z}}\log {\frac {1}{1-z}}\right)\right)^{\delta }&={\frac {1}{2\pi i}}\int _{C}(1-z)^{\alpha }\left({\frac {1}{z}}\log {\frac {1}{1-z}}\right)^{\gamma }\left({\frac {1}{z}}\log \left({\frac {1}{z}}\log {\frac {1}{1-z}}\right)\right)^{\delta }{\frac {dz}{z^{n+1}}}\\&={\frac {1}{2\pi i}}\int _{H_{\frac {1}{n}}}(1-z)^{\alpha }\left({\frac {1}{z}}\log {\frac {1}{1-z}}\right)^{\gamma }\left({\frac {1}{z}}\log \left({\frac {1}{z}}\log {\frac {1}{1-z}}\right)\right)^{\delta }{\frac {dz}{z^{n+1}}}\\&={\frac {n^{-a-1}}{2\pi i}}(\log n)^{\gamma }(\log \log n)^{\delta }\int _{H_{1}}(-t)^{\alpha }\left(1+{\frac {t}{n}}\right)^{-n-1}dt\\&\sim {\frac {n^{-a-1}}{2\pi i}}(\log n)^{\gamma }(\log \log n)^{\delta }\int _{H_{1}}(-t)^{\alpha }e^{-t}dt\\&={\frac {n^{-\alpha -1}}{\Gamma (-\alpha )}}(\log n)^{\gamma }(\log \log n)^{\delta }\end{aligned}}}](../_assets_/eb734a37dd21ce173a46342d1cc64c92/f80539422d7a81377aad4432135981803a525bd0.svg)
Singularity Analysis
Explanation and example from Flajolet and Sedgewick[7].
In the below

Little o
We will be making use of the "little o" notation.
 as
as 
which means

It also means for each  there exists
there exists  such that[8]
such that[8]

a fact we will use in the proof.
It is also useful to note

Summary
For the generating function  :
:
- Find
 's singularity
's singularity  .
.
- Construct the
 -domain at
-domain at  .
.
- Check that
 is analytic in the
is analytic in the  -domain.
-domain.
- Create an approximation of
 near
near  of the form
of the form  .
.
- The estimate of
![{\displaystyle [(z/\zeta )^{n}]f(z)\sim {\frac {n^{-\alpha -1}}{\Gamma (-\alpha )}}(\log n)^{\gamma }(\log \log n)^{\delta }}](../_assets_/eb734a37dd21ce173a46342d1cc64c92/45c2718c21e953c50afadcc8dbafb37a7712754d.svg) or equivalently
or equivalently ![{\displaystyle [z^{n}]f(z)\sim \zeta ^{-n}{\frac {n^{-\alpha -1}}{\Gamma (-\alpha )}}(\log n)^{\gamma }(\log \log n)^{\delta }}](../_assets_/eb734a37dd21ce173a46342d1cc64c92/31699e0ef2e1241b287e9ccb970500be45337b86.svg) .
.
Details
As an example, we will use  . It has a branch point singularity at
. It has a branch point singularity at  .
.
The  -domain at 1 is a circle centred at the origin with radius
-domain at 1 is a circle centred at the origin with radius  with a triangle cut out of it with one vertex at 1 and edges of angles
with a triangle cut out of it with one vertex at 1 and edges of angles  and
and  . See image below. We use this domain as it allows us to make a proof later.
. See image below. We use this domain as it allows us to make a proof later.
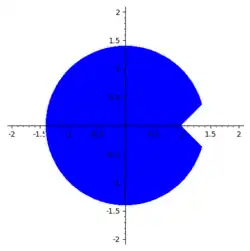
For  to be analytic in the
to be analytic in the  -domain:
-domain:

for all  in the
in the  -domain[9].
-domain[9].
Our example is analytic in the  -domain because
-domain because
 is an entire function (i.e. has no singularities), which means it is analytic everywhere.
is an entire function (i.e. has no singularities), which means it is analytic everywhere. is analytic except for the slit along the real axis for
is analytic except for the slit along the real axis for  .
.- The product of two analytic functions is an analytic function on the same domain[10]. Therefore,
 is analytic on the entire complex domain, including the
is analytic on the entire complex domain, including the  -domain, except for the real axis
-domain, except for the real axis  .
.
We want an approximation of the form  (where in our example we set
(where in our example we set  and
and  ).
).
Normally, this will be in the form of a Taylor series expansion.
For our example, doing the Taylor Expansion near to 1:



Therefore:

Then ![{\displaystyle [z^{n}]f(z)\sim {\frac {n^{-\alpha -1}}{\Gamma (-\alpha )}}(\log n)^{\gamma }(\log \log n)^{\delta }}](../_assets_/eb734a37dd21ce173a46342d1cc64c92/5467db6609038867e443189b46cbf6400d6a85f7.svg) .
.
Therefore, in our example:
![{\displaystyle [z^{n}]{\frac {e^{-z/2-z^{2}/4}}{\sqrt {1-z}}}\sim {\frac {e^{-3/4}}{\sqrt {\pi n}}}}](../_assets_/eb734a37dd21ce173a46342d1cc64c92/73b5c7c3ed02f1f3fe6a788e2713d380d18215b0.svg)
The proof of this comes from the fact that:
![{\displaystyle [z^{n}]f(z)=\zeta ^{-n}[(z/\zeta ^{n}]f(z)}](../_assets_/eb734a37dd21ce173a46342d1cc64c92/8a22bbb9a763463fb2bd4a38e0f80327ab99ddbd.svg)
![{\displaystyle [(z/\zeta )^{n}]f(z)=[(z/\zeta )^{n}]F(z/\zeta )+[(z/\zeta )^{n}]o(F(z/\zeta ))}](../_assets_/eb734a37dd21ce173a46342d1cc64c92/85f2a1a89156689276e5c73360f08ed58882f5c3.svg)
- the coefficients of the first term
![{\displaystyle [(z/\zeta )^{n}]F(z/\zeta )\sim {\frac {n^{-\alpha -1}}{\Gamma (-\alpha )}}(\log n)^{\gamma }(\log \log n)^{\delta }}](../_assets_/eb734a37dd21ce173a46342d1cc64c92/be6aa41d20fc3f05dabeb44eec4111a381055888.svg) , which we get from the standard function scale.
, which we get from the standard function scale.
- and the coefficients of the second term
![{\displaystyle [(z/\zeta )^{n}]o(F(z/\zeta ))=o\left(n^{-\alpha -1}(\log n)^{\gamma }(\log \log n)^{\delta }\right)}](../_assets_/eb734a37dd21ce173a46342d1cc64c92/779c8f833991f3406b3e2b29c1bc7306d9b60674.svg) which we do in #Proof of error term. This is also the reason why we need to use the
which we do in #Proof of error term. This is also the reason why we need to use the  -domain.
-domain.
Proof of error term
Proof from Flajolet and Odlyzko[11], Flajolet and Sedgewick[12] and Pemantle and Wilson[13].
We get the estimate of the coefficient for the second term from Cauchy's coefficient formula:
![{\displaystyle [z^{n}]o(F(z))={\frac {1}{2i\pi }}\int _{\gamma }o(F(z)){\frac {dz}{z^{n+1}}}}](../_assets_/eb734a37dd21ce173a46342d1cc64c92/9bab9adb952833a388dbf94e2a231299603cd31a.svg)
where  is any closed contour inside the
is any closed contour inside the  -domain. See the red line in the image below.
-domain. See the red line in the image below.
We split  into four parts such that
into four parts such that  .
.






Contribution of  :
:
The maximum of  on
on  is when
is when 

The maximum of  on
on  is
is

The maximum of  on
on  is
is 

Contribution of  and
and  :
:
We parameterise the contour  by converting
by converting  to polar form by
to polar form by  , so that
, so that  is a function of
is a function of  from
from  to
to  .
.  is the positive solution to the equation
is the positive solution to the equation  , so that the contour joins
, so that the contour joins  :
:

But, remember that the little o relation only holds within a particular  of
of  . We know that
. We know that  tends to zero as
tends to zero as  increases, and therefore, for any
increases, and therefore, for any  , we choose an
, we choose an  big enough so that
big enough so that  . We split the integral above into two at
. We split the integral above into two at  , so that
, so that  :
:

The first term in the sum:

 [14] (where
[14] (where  is the real part of x).
is the real part of x).

This converges to a constant  . Therefore:
. Therefore:

The second term in the sum:

 grows faster with
grows faster with  than
than  , so
, so  as
as  . Therefore:
. Therefore:

A similar argument applies to  .
.
Contribution of  :
:
By Cauchy's inequality

meaning the contribution of the integral around  is exponentially small as
is exponentially small as  and can be discarded.
and can be discarded.
The above assumes only one singularity  . But, it can be generalised for functions with multiple singularities.
. But, it can be generalised for functions with multiple singularities.
In the case of multiple singularities, the separate contributions from each of the singularities, as given by the basic singularity analysis process, are to be added up.
—Flajolet and Sedgewick 2009, pp. 398.
Theorem from Flajolet and Sedgewick[15].
Assume  is analytic on the disc
is analytic on the disc  , has a finite number of singularities on the circle
, has a finite number of singularities on the circle  and
and  is analytic on the
is analytic on the  -domain with multiple indents, one at each singularity.
-domain with multiple indents, one at each singularity.
If for each singularity  (for
(for  ):
):

then:
![{\displaystyle [z^{n}]f(z)\sim \sum _{i=0}^{r}\zeta _{i}^{n}{\frac {n^{-{\alpha _{i}}-1}}{\Gamma (-{\alpha _{i}})}}(\log n)^{\gamma _{i}}(\log \log n)^{\delta _{i}}\quad ({\text{as }}n\to \infty )}](../_assets_/eb734a37dd21ce173a46342d1cc64c92/7a81360f672166162061d70a2ffe154b1964c6fd.svg)
Notes
- ↑ Flajolet and Odlyzko 1990, pp. 14.
- ↑ Flajolet and Sedgewick 2009, pp. 393.
- ↑ Sedgewick, pp. 16. Flajolet and Sedgewick 2009, pp. 381. Flajolet and Odlyzko 1990, pp. 4-15.
- ↑ Lorenz 2011.
- ↑ For more details, see Flajolet and Odlyzko 1990, pp. 12-15.
- ↑ Sedgewick, pp. 10.
- ↑ Flajolet and Sedgewick 2009, pp. 392-395.
- ↑ Flajolet and Odlyzko 1990, pp. 8.
- ↑ Lang 1999, pp. 68-69.
- ↑ Lang 1999, pp. 69.
- ↑ Flajolet and Odlyzko 1990, pp. 7-9.
- ↑ Flajolet and Sedgewick 2009, pp. 390-392.
- ↑ Pemantle and Wilson 2013, pp. 59-60.
- ↑ w:Polar_coordinate_system#Converting_between_polar_and_Cartesian_coordinates.
- ↑ Flajolet and Sedgewick 2009, pp. 398.
References
- Flajolet, Philippe; Odlyzko, Andrew (1990). "Singularity analysis of generating functions" (PDF). SIAM Journal on Discrete Mathematics. 1990 (3).
- Flajolet, Philippe; Sedgewick, Robert (2009). Analytic Combinatorics (PDF). Cambridge University Press.
- Lang, Serge (1999). Complex Analysis (4th ed.). Springer Science+Business Media, LLC.
- Lorenz, Dirk (2011). "Substitution and integration by parts for functions of a complex variable". Retrieved 27 November 2022.
- Pemantle, Robin; Wilson, Mark C. (2013). Analytic Combinatorics in Several Variables (PDF). Cambridge University Press.
- Sedgewick, Robert. "6. Singularity Analysis" (PDF). Retrieved 13 November 2022.
- Stroud, K. A. (2003). Advanced Engineering Mathematics (4th ed.). Palgrave Macmillan.







