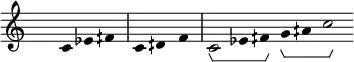Quarter-Tone Harmony/Scales

Artificial quarter-tone scales are entirely possible, and can be theoretically used in the same ways that the major or minor scales can be used. To be specific, in Wyschnegradsky's words...

That is to say, all the notes of the scale are treated as real notes and others as accidentals.

The scales that will be discussed here are exclusively those that repeat (in some form) at the octave, as scales in Western music typically do. Scales that repeat at intervals other than the octave are possible, but will not be discussed here.

Wyschnegradsky's Categorization

Wyschnegradsky categorizes quarter-tone scales into three main groups.

Regular and Semi-regular Scales

The first type, regular scales, divide the octave into equal pieces. In the quarter-tone system, leaving out scales of less than five tones, only four regular scales exist:

  1. The whole tone scale, six equal steps
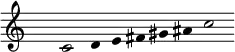
    \fixed c' { \hide Staff.TimeSignature \hide Staff.Stem \hide Staff.Beam \hide Score.BarNumber \accidentalStyle modern \cadenzaOn c2 d4 e fs gs as c'2 }
  2. The three-quarter-tones scale, eight equal steps
    \fixed c' { \hide Staff.TimeSignature \hide Staff.Stem \hide Staff.Beam \hide Score.BarNumber \accidentalStyle modern \cadenzaOn c2 dqf4 ef fqf gf gqs a bqf c'2 }
  3. The typical chromatic scale, twelve equal steps
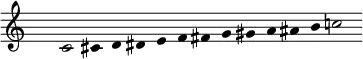
    \fixed c' { \hide Staff.TimeSignature \hide Staff.Stem \hide Staff.Beam \hide Score.BarNumber \accidentalStyle modern \cadenzaOn c2 cs4 d ds e f fs g gs a as b c'2 }
  4. The quartertonal chromatic scale, twenty-four equal steps
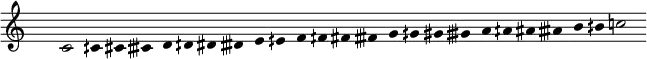
    \fixed c' { \hide Staff.TimeSignature \hide Staff.Stem \hide Staff.Beam \hide Score.BarNumber \accidentalStyle modern \cadenzaOn c2 cqs4 cs ctqs d dqs ds dtqs e eqs f fqs fs ftqs g gqs gs gtqs a aqs as atqs b bqs c'2 }

The second category, semi-regular scales, consists of specific scales that are based off an equal division of the octave—into two, three, four, six, or eight equal parts in the quarter-tone system—such that each division is further divided irregularly, but in the same fashion.

\fixed c' { \hide Staff.TimeSignature \hide Staff.Stem \hide Staff.Beam \hide Score.BarNumber \accidentalStyle modern \cadenzaOn c2 dqf4 dqs e2 fqs4 gqf af2 aqs4 bqf c'2 }

For example, the semi-regular scale above is based on the division of the octave into three major thirds, and each of them is further divided into a tetrachord in a pattern of neutral second, semitone, and then neutral second.

\fixed c' { \hide Staff.TimeSignature \hide Staff.Stem \hide Staff.Beam \hide Score.BarNumber \accidentalStyle modern \cadenzaOn c2 cqs4 dqs ef2 eqf4 fqs4 fs2 gqf4 aqf a2 aqs4 bqs c'2 }

This similar semi-regular scale divides the octave into four minor thirds, each of which is further divided in a pattern of quartertone, semitone, quartertone.

Irregular Scales

The third category of scales, irregular scales, consists of any scale which is not regular or semi-regular. This category, however, is so broad that it is in need of organization.

To do so, we use the principles of tetrachords which form our own Western scales. Tetrachords are series of four notes that span a perfect fourth. Two tetrachords combine to form a scale when the second tetrachord starts a perfect fifth above the first. For example, the major scale is constructed by two congruent tetrachords:

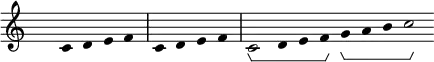
\layout{\context{\Voice\consists Horizontal_bracket_engraver}} \fixed c' { \hide Staff.TimeSignature \hide Staff.Stem \hide Staff.Beam \hide Score.BarNumber \accidentalStyle forget \cadenzaOn c4 d e f \bar"|" c d e f \bar"|" c2\startGroup d4 e f\stopGroup g\startGroup a b c'2\stopGroup }

The minor scales can be constructed similarly, although the two tetrachords are different:

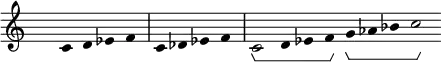
\layout{\context{\Voice\consists Horizontal_bracket_engraver}} \fixed c' { \hide Staff.TimeSignature \hide Staff.Stem \hide Staff.Beam \hide Score.BarNumber \accidentalStyle forget \cadenzaOn c4 d ef f \bar"|" c df ef f \bar"|" c2\startGroup d4 ef f\stopGroup g\startGroup af bf c'2\stopGroup }

Already this presents various opportunities for incorporating quartertones.

  • Modifying the intervals that comprise tetrachords to include quartertones
  • Changing the quanitity of tones within a tetrachord, which produce trichords (three notes), pentachords (five notes), hexachords (six notes), heptachords (seven notes), etc.
  • Changing the size of the interval of the outer two tones from a perfect fourth
  • Changing how the tetrachords combine to form a scale

This allows for an infinite variety of irregular scales. Here are some examples by Wyshcnegradsky:

\layout{\context{\Voice\consists Horizontal_bracket_engraver}} \fixed c' { \hide Staff.TimeSignature \hide Staff.Stem \hide Staff.Beam \hide Score.BarNumber \accidentalStyle forget \cadenzaOn c4 dqf eqf f \bar"|" c dqf etqf fqf \bar"|" c2\startGroup dqf4 eqf f\stopGroup gqs\startGroup a bf c'2\stopGroup }
\layout{\context{\Voice\consists Horizontal_bracket_engraver}} \fixed c' { \hide Staff.TimeSignature \hide Staff.Stem \hide Staff.Beam \hide Score.BarNumber \accidentalStyle forget \cadenzaOn c4 dqf ef eqs fqs \bar"|" c dqf eqs fs \bar"|" c2\startGroup dqf4 ef eqs fqs\stopGroup gf\startGroup atqf bqf c'2\stopGroup }
\layout{\context{\Voice\consists Horizontal_bracket_engraver}} \fixed c' { \hide Staff.TimeSignature \hide Staff.Stem \hide Staff.Beam \hide Score.BarNumber \accidentalStyle forget \cadenzaOn c4 ef fqs \bar"|" c dqs f \bar"|" c2\startGroup ef4 fqs\stopGroup g\startGroup aqs c'2\stopGroup }
This article is issued from Wikibooks. The text is available under Creative Commons Attribution-Share Alike 4.0 unless otherwise noted. Additional terms may apply for the media files.